题目内容
设正整数数列{an}满足a1=2,a2=6,当n≥2时,有|| a | 2 n |
| 1 |
| 2 |
(1)求a3的值;(2)求数列{an}的通项;
(3)记Tn=
| 12 |
| a1 |
| 22 |
| a2 |
| 32 |
| a3 |
| n2 |
| an |
| 9 |
| 4 |
分析:(1)n=2时,|
-a1a3| <
a1,利用条件a1=2,a2=6,得|36-2a3|<1,结合正整数数列{an},可求;
(2)先猜后证,关键是第二步的证明,必须利用归纳假设;
(3)通过两次等式相减,利用错位相减法求和,从而可证.
| a | 2 2 |
| 1 |
| 2 |
(2)先猜后证,关键是第二步的证明,必须利用归纳假设;
(3)通过两次等式相减,利用错位相减法求和,从而可证.
解答:解:(1)n=2时,|
-a1a3| <
a1,由已知a1=2,a2=6,得|36-2a3|<1,因为正整数数列{an},所以a3=18;
(2)猜想an=2×3n-1,下面用数学归纳法证明
①n=1,2时成立
②假设时n=k成立,即ak=2×3k-1,则ak-1=2×3k-2,于是|
-an-1an+1| <
an-1整理结合归纳假设得|2×3k-ak+1 | <
,因为正整数数列{an},所以ak+1=2×3k,即n=k+1时成立
综上知an=2×3n-1
(2)证明:由2Tn=1+
+
++
②得
Tn=
+
++
+
③
②-③得:
Tn=
+
++
-
④
∴
Tn=
+
++
-
-
⑤
④-⑤式得:
Tn=
+
++
-
-
+
| a | 2 2 |
| 1 |
| 2 |
(2)猜想an=2×3n-1,下面用数学归纳法证明
①n=1,2时成立
②假设时n=k成立,即ak=2×3k-1,则ak-1=2×3k-2,于是|
| a | n 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上知an=2×3n-1
(2)证明:由2Tn=1+
| 22 |
| 3 |
| 32 |
| 32 |
| n2 |
| 3n-1 |
| 2 |
| 3 |
| 12 |
| 3 |
| 22 |
| 3 |
| (n-1)2 |
| 3n-1 |
| n2 |
| 3n |
②-③得:
| 4 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
| 2n-1 |
| 3n-1 |
| n2 |
| 3n |
∴
| 4 |
| 9 |
| 1 |
| 3 |
| 2 |
| 32 |
| 2n-3 |
| 3n-1 |
| 2n-1 |
| 3n |
| n2 |
| 3n+1 |
④-⑤式得:
| 8 |
| 9 |
| 1 |
| 3 |
| 2 |
| 32 |
| 2 |
| 3n-1 |
| 2n-1 |
| 3n |
| n2 |
| 3n |
| n2 |
| 3n+1 |
|
点评:本题考查数列知识的综合运用,解题时要认真审题,注意挖掘题设中的隐含条件.

练习册系列答案
相关题目
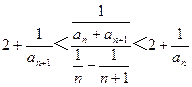 .
.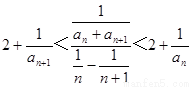 .
.