题目内容
设正整数数列{an}满足:a2=4,且对于任何n∈N*,有2+| 1 |
| an+1 |
| ||||
|
| 1 |
| an |
(1)求a1,a3;
(2)求数列{an}的通项an.
分析:(1)令n=1,根据2+
<
<2+
可得到
<a1<
,再由a1为正整数可得到a1的值,当n=2时同样根据2+
<
<2+
可得到2+
<6(
+
)<2+
进而可得到a3的范围,最后根据数列{an}是正整数数列求出a3的值.
(2)先根据a1=1,a2=4,a3=9可猜想an=n2,再用数学归纳法证明.
| 1 |
| an+1 |
| ||||
|
| 1 |
| an |
| 2 |
| 3 |
| 8 |
| 7 |
| 1 |
| an+1 |
| ||||
|
| 1 |
| an |
| 1 |
| a3 |
| 1 |
| 4 |
| 1 |
| a3 |
| 1 |
| 4 |
(2)先根据a1=1,a2=4,a3=9可猜想an=n2,再用数学归纳法证明.
解答:解:(1)据条件得2+
<n(n+1)(
+
)<2+
①
当n=1时,由2+
<2(
+
)<2+
,即有2+
<
+
<2+
,
解得
<a1<
.因为a1为正整数,故a1=1.
当n=2时,由2+
<6(
+
)<2+
,解得8<a3<10,所以a3=9.
(2)由a1=1,a2=4,a3=9,猜想:an=n2.
下面用数学归纳法证明.
①当n=1,2时,由(1)知an=n2均成立;
②假设n=k(k≥2)成立,则ak=k2,则n=k+1时
由(1)得2+
<k(k+1)(
+
)<2+
∴
<ak+1<
<ak+1<
,
即
<ak+1<
∴(k+1)2-
<ak+1<(k+1)2+
因为k≥2时,(k3+1)-(k+1)2=k(k+1)(k-2)≥0,所以
∈(0,1].
k-1≥1,所以
∈(0,1].又ak+1∈N*,所以(k+1)2≤ak+1≤(k+1)2.
故ak+1=(k+1)2,即n=k+1时,an=n2成立.由1°,2°知,对任意n∈N*,
an=n2.
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| an+1 |
| 1 |
| an |
当n=1时,由2+
| 1 |
| a2 |
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a1 |
| 1 |
| 4 |
| 2 |
| a1 |
| 2 |
| 4 |
| 1 |
| a1 |
解得
| 2 |
| 3 |
| 8 |
| 7 |
当n=2时,由2+
| 1 |
| a3 |
| 1 |
| 4 |
| 1 |
| a3 |
| 1 |
| 4 |
(2)由a1=1,a2=4,a3=9,猜想:an=n2.
下面用数学归纳法证明.
①当n=1,2时,由(1)知an=n2均成立;
②假设n=k(k≥2)成立,则ak=k2,则n=k+1时
由(1)得2+
| 1 |
| ak+1 |
| 1 |
| k2 |
| 1 |
| ak+1 |
| 1 |
| k2 |
∴
| k3(k+1) |
| k2-k+1 |
| k(k2+k-1) |
| k-1 |
| (k3+1-1)(k+1)2 |
| k3+1 |
| k[(k2+k)2-1] |
| k3-1 |
即
| (k3+1-1)(k+1)2 |
| k3+1 |
| k3(k+1)2-k |
| k3-1 |
∴(k+1)2-
| (k+1)2 |
| k3+1 |
| 1 |
| k-1 |
因为k≥2时,(k3+1)-(k+1)2=k(k+1)(k-2)≥0,所以
| (k+1)2 |
| k3+1 |
k-1≥1,所以
| 1 |
| k-1 |
故ak+1=(k+1)2,即n=k+1时,an=n2成立.由1°,2°知,对任意n∈N*,
an=n2.
点评:本题主要考查根据条件求数列的项和求数列的通项公式.先猜想数列的通项公式再由数学归纳法证明来求数列的通项公式的方法是高考的一个重要考点,要熟练掌握.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
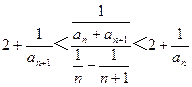 .
.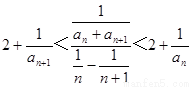 .
.