题目内容
如图1,矩形CDEF中DF=2CD=2,将平面ABCD沿着中线AB折成一个直二面角(如图2),点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
).
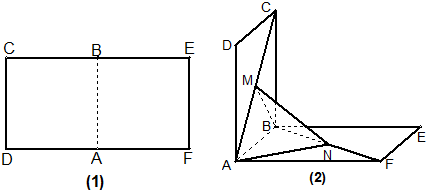
(1)求MN的长;
(2)当a为何值时,MN的长最小;
(3)当MN长最小时,求面MNA与面MNB所成的钝二面角α的余弦值.
| 2 |

(1)求MN的长;
(2)当a为何值时,MN的长最小;
(3)当MN长最小时,求面MNA与面MNB所成的钝二面角α的余弦值.
考点:与二面角有关的立体几何综合题,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(1)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连结PQ,依题意可得MNQP是平行四边形,由此能求出MN的长.
(2)由已知得当M、N分别移动到AC、BF的中点时,MN的长最小,最小值为
.
(3)取MN的中点G,连结AG、BG,∠AGB即为二面角α的平面角,由此能求出面MNA与面MNB所成的钝二面角α的余弦值.
(2)由已知得当M、N分别移动到AC、BF的中点时,MN的长最小,最小值为
| ||
| 2 |
(3)取MN的中点G,连结AG、BG,∠AGB即为二面角α的平面角,由此能求出面MNA与面MNB所成的钝二面角α的余弦值.
解答:
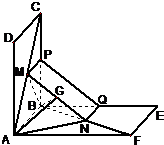 解:(1)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,
解:(1)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,
连结PQ,依题意可得MP∥NQ,且MP=NQ,
即MNQP是平行四边形,
∴MN=PQ.由已知,CM=BN=a,CB=AB=BE=1,
∴AC=BF=
,
=
,
=
.
即CP=BQ=
.
∴MN=PQ=
=
=
(0<a<
).…(5分)
(2)由(Ⅰ),MN=
,
∴当a=
时,MN=
.
即M、N分别移动到AC、BF的中点时,
MN的长最小,最小值为
.…(8分)
(3)取MN的中点G,连结AG、BG,
∵AM=AN,BM=BN,G为MN的中点
∴AG⊥MN,BG⊥MN,∠AGB即为二面角α的平面角,…(10分)
又AG=BG=
,
∴由余弦定理有cosα=
=-
.
故所求二面角的余弦值为-
…(12分)
 解:(1)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,
解:(1)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连结PQ,依题意可得MP∥NQ,且MP=NQ,
即MNQP是平行四边形,
∴MN=PQ.由已知,CM=BN=a,CB=AB=BE=1,
∴AC=BF=
| 2 |
| CP |
| 1 |
| a | ||
|
| BQ |
| 1 |
| a | ||
|
即CP=BQ=
| a | ||
|
∴MN=PQ=
| (1-CP)2+BQ2 |
(1-
|
=
(a-
|
| 2 |
(2)由(Ⅰ),MN=
(a-
|
∴当a=
| ||
| 2 |
| ||
| 2 |
即M、N分别移动到AC、BF的中点时,
MN的长最小,最小值为
| ||
| 2 |
(3)取MN的中点G,连结AG、BG,
∵AM=AN,BM=BN,G为MN的中点
∴AG⊥MN,BG⊥MN,∠AGB即为二面角α的平面角,…(10分)
又AG=BG=
| ||
| 4 |
∴由余弦定理有cosα=
(
| ||||||||
2•
|
| 1 |
| 3 |
故所求二面角的余弦值为-
| 1 |
| 3 |
点评:本题考查线段长的最小值的求法,考查二面角的余弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
如果实数x,y满足条件
,那么2x-y的最大值为( )
|
| A、-1 | B、-2 | C、2 | D、1 |
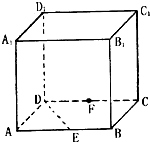 正方体ABCD-A1B1C1D1的棱长为a,E是棱AB的中点,F是棱CD的中点.
正方体ABCD-A1B1C1D1的棱长为a,E是棱AB的中点,F是棱CD的中点.