Question

已知在直三棱柱ABC-A₁B₁C₁中，棱AB，BC，BB₁两两垂直且长度相等，点P在线段A₁C₁（包括端点A₁，C₁）上运动，直线BP与B₁C所成角为θ，则θ的取值范围是（　　）

• A、0＜θ≤

  π

  2

• B、

  π

  6

  ≤θ≤

  π

  2

• C、

  π

  3

  ≤θ≤

  π

  2

• D、0＜θ≤

  π

  3

Answer 1

考点：异面直线及其所成的角

专题：空间角,空间向量及应用

分析：画出图形，建立空间直角坐标系，设棱长AB=1，P（-a，1-a，1）（0≤a≤1），
求出

BP

、

B1C

的坐标表示，利用空间向量的夹角公式，求出结果．

解答： 解：画出图形，建立空间直角坐标系，如图所示；
设棱长AB=1，

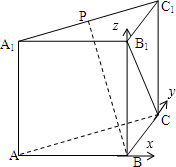
则B（0，0，0），C（0，1，0），B₁（0，0，1），
设P（-a，1-a，1）（0≤a≤1），
则

BP

=（-a，1-a，1），

B1C

=（0，1，-1），
∴cosθ=|

BP • B1C

| BP |×| B1C |

|
=|

-a×0+(1-a)×1+1×(-1)

(-a)2+(1-a)2+1 × 2

|
=

a

2 a2-a+1

，
当a=0时，cosθ=0，
当a≠0时，cosθ=

1

2

•

1

1- 1 a + 1 a2

=

1

2

•

1

( 1 a - 1 2 )2+ 3 4

；
∵0＜a≤1，
∴

1

a

≥1，
∴

( 1 a - 1 2 )2+ 3 4

≥1，当且仅当a=1时“=”成立；
∴cosθ≤

1

2

，即0≤cosθ≤

1

2

；
又∵0≤θ≤

π

2

，
∴

π

3

≤θ≤

π

2

，
即θ的取值范围是

π

3

≤θ≤

π

2

．
故选：C．

点评：本题考查了利用空间向量的知识求空间角的问题，解题时建立适当的坐标系是解题的关键，属于中档题．