题目内容
19．设函数$f（x）=\frac{1}{2}{x^2}-4lnx$（Ⅰ）求f（x）的单调区间；
（Ⅱ）求f（x）在区间[1，e]上的最值．
分析 （Ⅰ）求出定义域，函数的导数，极值点，利用导函数的符号求f（x）的单调区间；
（Ⅱ）利用函数的极值以及端点函数值，求解函数的最值即可．
解答 解：（I）定义域为（0，+∞）…（2分）
得$f'（x）=x-\frac{4}{x}$，令f'（x）=0，x=2
| x | 0＜x＜2 | x＞2 |
| f'（x） | - | + |
（ II）由（I），f（x）在[1，2]减，在[2，e]增，
所以f（x）min=f（2）=2-4ln2…（9分）
又f（1）=$\frac{1}{2}$，$f（e）=\frac{1}{2}{e^2}-4$…（11分）
因为$f（e）=\frac{1}{2}{e^2}-4＜\frac{1}{2}$
所以f（x）min=f（2）=2-4ln2，$f{（x）_{max}}=\frac{1}{2}$…（14分）
点评 本题考查函数的导数的综合应用，函数的最值以及函数的单调性极值的求法，考查转化思想以及计算能力．
练习册系列答案
期末1卷素质教育评估卷系列答案
相关题目
14．下列说法正确的是（ ）
| A． | 函数y=|x|有极大值，但无极小值 | B． | 函数y=|x|有极小值，但无极大值 | ||
| C． | 函数y=|x|既有极大值又有极小值 | D． | 函数y=|x|无极值 |
11．已知函数f（x）=xln x，g（x）=（-x2+ax-3）ex（a为实数）．
（1）当a=5时，求函数y=g（x）在x=1处的切线方程；
（2）求f（x）在区间[t，t+2]（t＞0）上的最小值．
（1）当a=5时，求函数y=g（x）在x=1处的切线方程；
（2）求f（x）在区间[t，t+2]（t＞0）上的最小值．
8．若一个正三棱锥的正（主）视图如图所示，则其体积等于（ ）
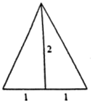
| A． | $\frac{{\sqrt{3}}}{6}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\frac{{2\sqrt{3}}}{3}$ | D． | $2\sqrt{3}$ |