题目内容

1．解不等式：x2-5ax+6a2＞0，a≠0．

分析 把不等式x2-5ax+6a2＞0化为（x-2a）（x-3a）＞0，讨论a＞0和a＜0时，求出不等式的解集即可．

解答 解：不等式x2-5ax+6a2＞0
即（x-2a）（x-3a）＞0，
∵a≠0，
当a＞0时，2a＜3a，
不等式的解集为{x|x＜2a 或x＞3a}；
当a＜0时，2a＞3a，
不等式的解集为{x|x＜3a 或x＞2a}．

点评 本题考查了含有字母系数的一元二次不等式的解法问题，是基础题目．

练习册系列答案
相关题目
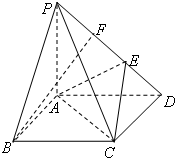8．已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点分别为A1，A2．，A1关于直线bx+ay=0的对称点在圆（x+a）2+y2=a2上，则椭圆的离心率为$\frac{\sqrt{2}}{2}$．
12．四棱锥P-ABCD的底面是边长为1的正方形，PA⊥CD，PA=1，PD=$\sqrt{2}$，E，F为PD上两点，且PF=ED=$\frac{1}{3}$PD．
（1）求证：BF∥面ACE；
（2）求异面直线PC与AE所成角的余弦值；
（3）求二面角P-AC-E的余弦值．
9．已知椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的一个焦点$F（\sqrt{3}，0）$，长轴顶点到点A（0，-2）的距离为2$\sqrt{2}$，O为坐标原点．
（1）求椭圆C的方程；
（2）设过A点的动直线l与椭圆C相交于M，N两点，当△OMN的面积最大时，求l的方程．
16．已知函数$f（x）=\frac{lnx}{x}$．
（1）求函数f（x）的单调区间；
（2）设m＞0，求f（x）在[m，2m]上的最大值．
6．已知函数f（x）=2x3-3x2-12x
（1）求f（x）=2x3-3x2-12x的极值；
（2）设函数g（x）=2x3-3x2-12x+a的图象与x轴有两个交点，求a的值．
13．设函数f（x）=2cos2x+$\sqrt{3}$sin2x．
（1）求函数f（x）的最小正周期和单调递增区间；
（2）求函数f（x）的最小值及x的取值集合．
10．设函数f（x）=ax-$\frac{a}{x}$-2lnx．
（Ⅰ）若f（x）在x=2时有极值，求实数a的值和f（x）的极大值；
（Ⅱ）若f（x）在定义域上是减函数，求实数a的取值范围．
11．已知函数f（x）=xln x，g（x）=（-x2+ax-3）ex（a为实数）．
（1）当a=5时，求函数y=g（x）在x=1处的切线方程；
（2）求f（x）在区间[t，t+2]（t＞0）上的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网