题目内容
在正方形ABCD-A1B1C1D1中，M，N，P分别是BC，CC1，CD的中点，求证：A1P⊥平面MDN．
考点：直线与平面垂直的判定
专题：空间位置关系与距离
分析：建立空间直角坐标系，得到所需向量的坐标，利用向量数量积为0，得到直线垂直．
解答：
证明：如图建立空间直角坐标系
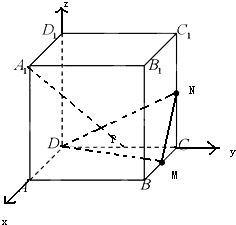
则D（0，0，0，），A1（2，0，2），M（1，2，0），N（0，2，1），P（0，1，0），
所以
=（-2，1，-2），
=（-1，0，1），
=（0，2，1），
所以
•
=2+0+2=0，
•
=0+2-2=0，
所以A1P⊥MN，A1P⊥DN，
所以A1P⊥平面MND．
则D（0，0，0，），A1（2，0，2），M（1，2，0），N（0，2，1），P（0，1，0），
所以
| A1P |
| MN |
| DN |
所以
| A1P |
| MN |
| A1P |
| DN |
所以A1P⊥MN，A1P⊥DN，
所以A1P⊥平面MND．
点评：本题开车了正方体为载体的线面垂直的判定定理的运用；在正方体中，线面关系的判断经常利用向量法解答，体现了向量的工具性．
练习册系列答案
相关题目
已知椭圆已知某几何体的三视图如如，则这个几何体为（ ）
| A、圆柱 | B、空心圆柱 | C、圆锥 | D、圆 |