题目内容
已知函数f(x)=-x3+ax2+b,(a,b∈R)
(1)若函数y=f(x)的图象切x轴于点(2,0),求a.b的值;
(2)设函数y=f(x)(x∈(0,1)) 的图象上任意一点的切线斜率为k,试求|k|≤1的充要条件;
(3)若函数y=f(x)的图象上任意不同的两点的连线斜率小于1,求a的取值范围.
(1)若函数y=f(x)的图象切x轴于点(2,0),求a.b的值;
(2)设函数y=f(x)(x∈(0,1)) 的图象上任意一点的切线斜率为k,试求|k|≤1的充要条件;
(3)若函数y=f(x)的图象上任意不同的两点的连线斜率小于1,求a的取值范围.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,导数的综合应用
分析:(1)求出函数的导数,求出切线的斜率,令f′(2)=0,f(2)=0,即可得到a,b;
(2)求出导数,对任意的x∈(0,1),|k|≤1,即|-3x2+2ax|≤1对任意的x∈(0,1)恒成立,运用参数分离,
等价于3x-
≤2a≤
+3x对任意的x∈(0,1)恒成立.令g(x)=
+3x,h(x)=3x-
,分别求出g(x),h(x)的最小值和最大值,解不等式即可得到;
(3)求出f(x)图象上任两点的斜率,列出不等式,化简整理,再令F(x)=f(x)-x,求出导数,再由二次函数的性质,得到判别式不大于0,解得即可.
(2)求出导数,对任意的x∈(0,1),|k|≤1,即|-3x2+2ax|≤1对任意的x∈(0,1)恒成立,运用参数分离,
等价于3x-
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
(3)求出f(x)图象上任两点的斜率,列出不等式,化简整理,再令F(x)=f(x)-x,求出导数,再由二次函数的性质,得到判别式不大于0,解得即可.
解答:
解:(1)函数f(x)=-x3+ax2+b的导数为:
f′(x)=-3x2+2ax,
由于函数y=f(x)的图象切x轴于点(2,0),
则f′(2)=0,即有-12+4a=0,解得,a=3,
f(2)=0,即有-8+3×4+b=0,解得,b=-4.
解得,a=3,b=-4;
(2)k=f′(x)=-3x2+2ax(0<x<1),
对任意的x∈(0,1),|k|≤1,即|-3x2+2ax|≤1对任意的x∈(0,1)恒成立,
等价于3x-
≤2a≤
+3x对任意的x∈(0,1)恒成立.
令g(x)=
+3x,h(x)=3x-
,
则
h(x)max≤a≤
g(x)min,x∈(0,1),
由于
+3x≥2
,当且仅当x=
时“=”成立,g(x)min=2
,
h(x)=3x-
在(0,1)上为增函数,h(x)max<2,
则1≤a≤
;
(3)设x1,x2∈R,且x1≠x2,k=
<1,
不妨设x1<x2,则f(x2)-x2<f(x1)-x1,
令F(x)=f(x)-x,则F(x)为R上的减函数,
则F′(x)=-3x2+2ax-1≤0对x∈R恒成立,
即3x2-2ax+1≥0对x∈R恒成立,
即△≤0,即4a2-12≤0,
则有-
≤a≤
.
f′(x)=-3x2+2ax,
由于函数y=f(x)的图象切x轴于点(2,0),
则f′(2)=0,即有-12+4a=0,解得,a=3,
f(2)=0,即有-8+3×4+b=0,解得,b=-4.
解得,a=3,b=-4;
(2)k=f′(x)=-3x2+2ax(0<x<1),
对任意的x∈(0,1),|k|≤1,即|-3x2+2ax|≤1对任意的x∈(0,1)恒成立,
等价于3x-
| 1 |
| x |
| 1 |
| x |
令g(x)=
| 1 |
| x |
| 1 |
| x |
则
| 1 |
| 2 |
| 1 |
| 2 |
由于
| 1 |
| x |
| 3 |
| ||
| 3 |
| 3 |
h(x)=3x-
| 1 |
| x |
则1≤a≤
| 3 |
(3)设x1,x2∈R,且x1≠x2,k=
| f(x2)-f(x1) |
| x2-x1 |
不妨设x1<x2,则f(x2)-x2<f(x1)-x1,
令F(x)=f(x)-x,则F(x)为R上的减函数,
则F′(x)=-3x2+2ax-1≤0对x∈R恒成立,
即3x2-2ax+1≥0对x∈R恒成立,
即△≤0,即4a2-12≤0,
则有-
| 3 |
| 3 |
点评:本题考查导数的运用:求切线方程和单调区间、极值和最值,考查不等式恒成立问题转化为求最值,考查函数的单调性的运用,考查运算能力,属于中档题和易错题.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
若关于x的不等式|x-1|<ax的解集中恰好有两个整数,则a的取值范围是( )
A、(
| ||||
B、(
| ||||
C、(
| ||||
| D、(-1,0) |
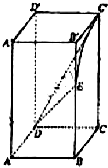 如图,四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=3
如图,四棱柱ABCD-A′B′C′D′中,底面ABCD为正方形,侧棱AA′⊥底面ABCD,AB=3| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
某办公室为保障财物安全,需在春节放假的七天内每天安排一人值班,已知该办公室共有四个人,每人需值班一天或两天,则不同的值班安排种数为( )
| A、360 | B、630 |
| C、2520 | D、15120 |
台风中心从A地以20km/h的速度向东偏北45°方向移动,离台风中心30km内的地区为危险区,城市B在A的正东40km处,B城市处于危险区内的时间为( )
| A、0.5h | B、1h |
| C、1.5h | D、2h |