题目内容
9. 已知正方体ABCD-A1B1C1D1中,E是BB1的中点
已知正方体ABCD-A1B1C1D1中,E是BB1的中点(1)求证:B1D∥平面ACE
(2)求异面直线CE与B1D所成角的余弦值.
分析 (1)根据线面平行转化为线线平行来证明即可.在平面ACE内找一个直线与B1D平行,连接BD交于O,连接OE,根据三角形中位线即可得证.
(2)由(1)可知B1D∥OE,异面直线CE与B1D所成角即为OE与CE所成角,即为∠OEC或补角.利用余弦定理求解.
解答 解:(1)由题意,ABCD-A1B1C1D1是正方体,E是BB1的中点,连接BD交于O,则O是DB的中点,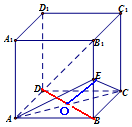
连接OE,
在三角形DBB1中,OE∥B1D,
∵OE?平面ACE.
∴B1D∥平面ACE.
(2)由(1)可知B1D∥OE,异面直线CE与B1D所成角即为OE与CE所成角,
即为∠OEC或补角,
∵BD⊥AC,
∴OE⊥AC,
∴△OEC是直角三角形.
设AB=CD=a,则OC=OB=$\frac{a\sqrt{2}}{2}$,BE=$\frac{a}{2}$,CE=$\frac{\sqrt{5}}{2}a$
∴OE=$\frac{\sqrt{3}a}{2}$.
∴cos∠OEC=$\frac{OE}{EC}$=$\frac{{\sqrt{15}}}{5}$.
点评 本题考查了线面平行的证明和异面直线所成角的求法.属于基础题.

练习册系列答案
相关题目
19.已知命题p:?x>0,都有(x+1)ex>1.则¬p为( )
| A. | ?x≤0,总有(x+1)ex≤1 | B. | ?x0>0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | ||
| C. | ?x0≤0,使得(x0+1)e${\;}^{{x}_{0}}$≤1 | D. | ?x>0,总有(x+1)ex≤1 |
 公园263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为24.
公园263年左右,我国数学家刘徽发现当圆内接正多边形的边数无限增加时,多边形面积可无限逼近圆的面积,并创立了“割圆术”.利用“割圆术”刘徽得到了圆周率精确到小数点后两位的近似值3.14,这就是著名的“徽率”.如图是利用刘徽的“割圆术”思想设计的一个程序框图,则输出n的值为24. 阅读如图所示的程序框图,运行相应程序,输出的结果是274.
阅读如图所示的程序框图,运行相应程序,输出的结果是274.