题目内容
19.设不等式组$\left\{\begin{array}{l}{0≤x≤3}\\{0≤y≤3}\end{array}\right.$表示的平面区域为P,不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{3x+2y-6≥0}\\{x≤2}\end{array}\right.$,表示的平面区域为Q(1)在区域P中任取一点M,求M∈Q的概率;
(2)在区域Q中任取一点N(x,y),求$\frac{y}{x}$≥$\frac{3}{4}$ 的概率.
分析 首先画出可行域,由题意,分别利用几何意义求出大圆区域的面积,利用面积比求概率.
解答 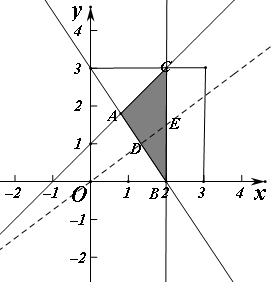 解:平面区域如图得到区域P的面积为9,不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{3x+2y-6≥0}\\{x≤2}\end{array}\right.$,
解:平面区域如图得到区域P的面积为9,不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{3x+2y-6≥0}\\{x≤2}\end{array}\right.$,
由$\left\{\begin{array}{l}{x-y+1=0}\\{3x+2y-6=0}\end{array}\right.$得到A($\frac{4}{5}$,$\frac{9}{5}$),所以平面区域为Q的面积为$\frac{1}{2}×3×(2-\frac{4}{5})=\frac{9}{5}$,
则(1)在区域P中任取一点M,求M∈Q的概率$\frac{\frac{9}{5}}{9}=\frac{1}{5}$;
(2)在区域Q中任取一点N(x,y),$\frac{y}{x}$≥$\frac{3}{4}$ 的区域如图中区域ACED,其中E(2,$\frac{3}{2}$),D($\frac{4}{3}$,1),
所以面积为$\frac{9}{5}-\frac{1}{2}×\frac{3}{2}×\frac{2}{3}=\frac{13}{10}$,所以所求概率为$\frac{\frac{13}{10}}{\frac{9}{5}}=\frac{13}{18}$.
点评 本题考查了简单线性规划问题以及几何概型的概率求法;明确目标函数的几何意义,利用面积比求概率.

练习册系列答案
相关题目
18.二项式(x+1)n(n∈N*)的展开式中x2项的系数为15,则n=( )
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
14.函数h(t)=-4.9t2+6.5t+10从0到2的平均变化率为( )
| A. | -2.2 | B. | -3.3 | C. | 2.2 | D. | 3.2 |
4.设有一个回归方程为$\stackrel{∧}{y}$=1-0.5x变量x增加一个单位时,则( )
| A. | y平均增加1.5个单位 | B. | y平均增加0.5个单位 | ||
| C. | y平均减少1.5个单位 | D. | y平均减少0.5个单位 |
8.已知函数$f(x)=lg({x+\sqrt{{x^2}+1}})+2x+sinx,f({x_1})+f({x_2})>0$,则下列不等式中正确的是( )
| A. | x1>x2 | B. | x1<x2 | C. | x1+x2<0 | D. | x1+x2>0 |
9.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0),有$\frac{{f({x_2})-f({x_1})}}{{{x_2}-{x_1}}}>0$,则( )
| A. | f(-4)<f(3)<f(-2) | B. | f(-2)<f(3)<f(-4) | C. | f(3)<f(-2)<f(-4) | D. | f(-4)<f(-2)<f(3) |