题目内容
4．抛物线y2=-4x的焦点坐标是（ ）| A． | （-2，0） | B． | （-1，0） | C． | （0，-1） | D． | （0，-2） |
分析 根据抛物线解析式，确定出焦点坐标即可．
解答 解：抛物线y2=-4x中，p=-2，
则焦点坐标为（-1，0），
故选：B．
点评 此题考查了抛物线的简单性质，熟练掌握抛物线的简单性质是解本题的关键．
练习册系列答案
相关题目
14．
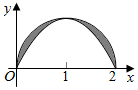如图，阴影部分由曲线f（x）=sin$\frac{π}{2}$x（0≤x≤2）与以点（1，0）为圆心，1为半径的半圆围成，现向半圆内随机投掷一点，恰好落在阴影部分内的概率为（ ）
如图，阴影部分由曲线f（x）=sin$\frac{π}{2}$x（0≤x≤2）与以点（1，0）为圆心，1为半径的半圆围成，现向半圆内随机投掷一点，恰好落在阴影部分内的概率为（ ）| A． | $\frac{4}{π}$-1 | B． | $\frac{8}{{π}^{2}}$ | C． | 1-$\frac{4}{π}$ | D． | 1-$\frac{8}{{π}^{2}}$ |
12．已知全集U={1，2，3，4，5，6}，集合A={2，4，5}，B={1，3，5}，则（∁UA）∪B=（ ）
| A． | {1} | B． | {3} | C． | {1，3，5，6} | D． | {1，3} |
9．设函数fn′（x）是fn（x）的导函数，f0（x）=ex（cosx+sinx），f1（x）=$\frac{f_0^'（x）}{{\sqrt{2}}}$，f2（x）=$\frac{f_1^'（x）}{{\sqrt{2}}}$，…，${f_{n+1}}（x）=\frac{f_n^'（x）}{{\sqrt{2}}}$（n∈N），则f2016（x）=（ ）
| A． | ex（cosx+sinx） | B． | ex（cosx-sinx） | C． | -ex（cosx+sinx） | D． | ex（sinx-cosx） |
16．已知集合A={x|-1≤x≤1}，B={x|x2-2x≤0}，则A∩B=（ ）
| A． | {x|-1≤x≤2} | B． | {x|-1≤x≤0} | C． | {x|1≤x≤2} | D． | {x|0≤x≤1} |