Question

【题目】已知函数和函数.

（1）若曲线在处的切线过点，求实数的值；

（2）求函数的单调区间；

（3）若不等式对于任意的恒成立，求实数的最大值.

Answer 1

【答案】（1）；（2）当时,单调递增区间为;

当时,单调增区间为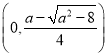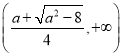，，单调递减区间为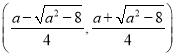；（3）2.

【解析】

(1)根据导数的几何意义求解即可.

(2)易得,再求导分析导函数分子的根的存在情况,进而可得导函数在区间上的正负以及原函数的单调性.

(3)令,再求导分析可得在上单调递增,可得.再分与两种情况分析函数的单调性求解最小值即可.

解（1）∵,∴,又∵,

曲线在处的切线方程为,

∵切线过点,∴,∴.

（2）的定义域为,

,则,令.

（Ⅰ）当即时,

∴函数的单调增区间为：.

（Ⅱ）当即或时,

有两个不等的实数根,,

当时,,,∴,

函数单调增区间为,

当时,,,

令,则或,

令,则,

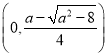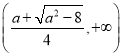∴单调递增区间为,,单调递减区间为.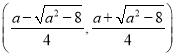

综上所述, 当时,单调递增区间为;

当时,单调增区间为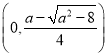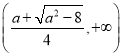，，单调递减区间为；

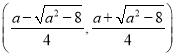（3）令,

则,

记,则,所以在上单调递增,

故,

当,,故在上单调递增,

所以,符合题意.

当时,,故,

又在上单调递增,所以存在唯一的实数,使得,

列表如下：

	-	0	+
		极小值

则当时,,这与恒成立矛盾.

综上,实数的最大值为2.