题目内容
【题目】已知抛物线![]() ,过点
,过点![]() 的直线
的直线![]() 交抛物线
交抛物线![]() 于
于![]() 两点.
两点.
(1)若直线![]() 平行于
平行于![]() 轴,
轴,![]() ,求抛物线
,求抛物线![]() 的方程;
的方程;
(2)对于(1)条件下的抛物线![]() ,当直线
,当直线![]() 的斜率变化时,证明
的斜率变化时,证明![]() .
.
【答案】(1)![]()
(2)证明见解析
【解析】
(1)由直线![]() 平行于
平行于![]() 轴可知
轴可知![]() 是以
是以![]() 为顶点的等腰三角形,联立直线
为顶点的等腰三角形,联立直线![]() 与抛物线的方程并利用三角形面积公式列方程,解得
与抛物线的方程并利用三角形面积公式列方程,解得![]() 的值,即得抛物线
的值,即得抛物线![]() 的方程;
的方程;
(2)联立直线![]() 与抛物线的方程,利用根与系数的关系及斜率公式得到
与抛物线的方程,利用根与系数的关系及斜率公式得到![]() ,即得
,即得![]() ,利用三角形面积公式得到线段比,即得证.
,利用三角形面积公式得到线段比,即得证.
解:(1)当直线![]() 平行于
平行于![]() 轴时,直线
轴时,直线![]() 的方程为
的方程为![]() 是以
是以![]() 为顶点的等腰三角形,
为顶点的等腰三角形,
联立方程,得![]() 消去
消去![]() 得
得![]() ,得
,得![]() .
.
所以![]() ,解得
,解得![]() ,
,
所以抛物线![]() 的方程为
的方程为![]() .
.
(2)欲证![]() ,
,
只需证![]() .
.
由题意可知直线![]() 的斜率
的斜率![]() 存在,
存在,
故可设直线![]() 的方程为
的方程为![]() ,
,
联立方程,得![]()
消去![]() ,得
,得![]() ,
,
则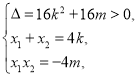
所以直线![]() 的斜率
的斜率![]() ,
,
直线![]() 的斜率
的斜率![]() ,
,
![]() ,
,
所以直线![]() 与
与![]() 的倾斜角互补,
的倾斜角互补,
所以![]() .
.
又![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() .
.

练习册系列答案
相关题目