题目内容
已知:
+
=
,求证:
+
=
.
| sin4θ |
| a |
| cos4θ |
| b |
| 1 |
| a+b |
| sin8θ |
| a3 |
| cos8θ |
| b3 |
| 1 |
| (a+b)3 |
考点:三角函数恒等式的证明
专题:证明题,三角函数的求值
分析:运用基本不等式可得,
+
≥2
,①
+
≥2
,②两式相加结合同角的平方关系,再由等号成立的条件可得sin2θ=
,cos2θ=
,将其代入要证的等式的左边,即可得证.
| sin4θ |
| a |
| a |
| (a+b)2 |
| sin2θ |
| a+b |
| cos4θ |
| b |
| b |
| (a+b)2 |
| cos2θ |
| a+b |
| a |
| a+b |
| b |
| a+b |
解答:
证明:由于a>0,b>0,
+
≥2
,①
+
≥2
,②
将①②两式相加并整理得,
+
+
≥
即为
+
≥
,③
由题设知,这三个不等式应同时取等号,
即有sin2θ=
,cos2θ=
,
则
+
=
+
=
+
=
=
.
则
+
=
.
| sin4θ |
| a |
| a |
| (a+b)2 |
| sin2θ |
| a+b |
| cos4θ |
| b |
| b |
| (a+b)2 |
| cos2θ |
| a+b |
将①②两式相加并整理得,
| sin4θ |
| a |
| cos4θ |
| b |
| a+b |
| (a+b)2 |
| 2 |
| a+b |
即为
| sin4θ |
| a |
| cos4θ |
| b |
| 1 |
| a+b |
由题设知,这三个不等式应同时取等号,
即有sin2θ=
| a |
| a+b |
| b |
| a+b |
则
| sin8θ |
| a3 |
| cos8θ |
| b3 |
| ||
| a3 |
| ||
| b3 |
=
| a |
| (a+b)4 |
| b |
| (a+b)4 |
| a+b |
| (a+b)4 |
=
| 1 |
| (a+b)3 |
则
| sin8θ |
| a3 |
| cos8θ |
| b3 |
| 1 |
| (a+b)3 |
点评:本题考查三角函数恒等式的证明,考查基本不等式的运用,考查同角的平方关系的运用,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
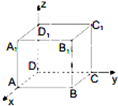 如图,把棱长为2的正方体ABCD-A1B1C1D1放在空间直角坐标系中,使D与原点重合,点A与点C分别放在x轴和y轴的正半轴上,则B1的坐标为:( )
如图,把棱长为2的正方体ABCD-A1B1C1D1放在空间直角坐标系中,使D与原点重合,点A与点C分别放在x轴和y轴的正半轴上,则B1的坐标为:( )| A、(2,2,2) |
| B、(2,2,0) |
| C、(2,0,2) |
| D、(0,2,2) |
设i是虚数单位,则复数z=i(-2+i)的虚部为( )
| A、-2 | B、-1 | C、-2i | D、2i |
复数z满足z(2+i)=2i,则在复平面内,复数z对应的点位于( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
若各项均为正数的数列{an}满足an-1=sinan(n∈N*),则下列说法中正确的是( )
| A、{an}是单调递减数列 |
| B、{an}是单调递增数列 |
| C、{an}可能是等差数列 |
| D、{an}可能是等比数列 |
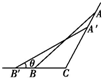 在△ABC中,角A、B、C所对的边分别是a、b、c,若∠C=
在△ABC中,角A、B、C所对的边分别是a、b、c,若∠C=