题目内容
设函数f(x)=(m+3)x2-4mx+2m-1,x∈R.
(I)若方程f(x)=0的两根异号,且负根的绝对值比正根大,求实数m的取值范围.
(Ⅱ)解不等式f(x)<(m+2)x2-2mx.
(I)若方程f(x)=0的两根异号,且负根的绝对值比正根大,求实数m的取值范围.
(Ⅱ)解不等式f(x)<(m+2)x2-2mx.
考点:一元二次方程的根的分布与系数的关系,一元二次不等式的解法
专题:函数的性质及应用
分析:(I)由条件利用二次函数的性质可得
,由此求得m的范围.
(Ⅱ)不等式即[x-(2m-1)]•(x-1)<0.再分当m>1时、当m=1时、当m<1时三种情况,分别求得不等式的解集.
|
(Ⅱ)不等式即[x-(2m-1)]•(x-1)<0.再分当m>1时、当m=1时、当m<1时三种情况,分别求得不等式的解集.
解答:
解:(I)由)=(m+3)x2-4mx+2m-1,方程f(x)=0的两根异号,且负根的绝对值比正根大,
可得
,即
,由此求得-3<m<0,
即实数m的取值范围为(-3,0).
(Ⅱ)不等式f(x)<(m+2)x2-2mx,即 x2-2mx-1<0,
即[x-(2m-1)]•(x-1)<0.
当m>1时,2m-1>1,不等式的解集为{x|1<x<2m-1};
当m=1时,2m-1=1,不等式的解集为∅;
当m<1时,2m-1<1,不等式的解集为{x|2m-1<x<1}.
可得
|
|
即实数m的取值范围为(-3,0).
(Ⅱ)不等式f(x)<(m+2)x2-2mx,即 x2-2mx-1<0,
即[x-(2m-1)]•(x-1)<0.
当m>1时,2m-1>1,不等式的解集为{x|1<x<2m-1};
当m=1时,2m-1=1,不等式的解集为∅;
当m<1时,2m-1<1,不等式的解集为{x|2m-1<x<1}.
点评:本题主要考查一元二次方程根的分布与系数的关系,二次函数的性质,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 如图,已知点F为抛物线C1:y2=4x的焦点,过点F任作两条互相垂直的直线l1,l2,分别交抛物线C1于A,C,B,D四点,E,G分别为AC,BD的中点.
如图,已知点F为抛物线C1:y2=4x的焦点,过点F任作两条互相垂直的直线l1,l2,分别交抛物线C1于A,C,B,D四点,E,G分别为AC,BD的中点.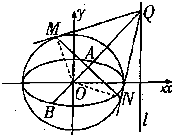 如图,已知椭圆
如图,已知椭圆