题目内容
已知椭圆C的中心在原点，一个焦点为F(0，
)，且长轴长与短轴长的比是∶1.
(1)求椭圆C的方程；
(2)若椭圆C上在第一象限的一点P的横坐标为1，过点P作倾斜角互补的两条不同的直线PA，PB分别交椭圆C于另外两点A， B，求证：直线AB的斜率为定值．
解析： (1)设椭圆C的方程为
＝1(a>b>0)．
由题意得
解得a2＝4，b2＝2.
所以椭圆C的方程为
＝1.
(2)证明：由题意知，两直线PA，PB的斜率必存在，设PB的斜率为k.又由(1)知，P(1，)，则直线PB的方程为y－＝k(x－1)．
由
得(2＋k2)x2＋2k(－k)x＋(－k)2－4＝0.
设A(xA，yA)，B(xB，yB)，
则xB＝1·xB＝
，
同理可得xA＝
，
则xA－xB＝
，yA－yB＝－k(xA－1)－k(xB－1)＝
.
所以kAB＝
＝为定值．
练习册系列答案
100分闯关期末冲刺系列答案
名校联盟快乐课堂系列答案
相关题目
＝1，
＝2，则AB边的长度为( )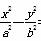
＝1(a＞0，b＞0)的一条渐近线交于一点M(1，m)，点M到抛物线焦点的距离为3，则双曲线的离心率等于( )
D.
.过F1的直线l交C于A，B两点，且△ABF2的周长为16，那么C的方程为________．
＋
＋
的最大值．
－
≥a＋
－2.
的值域．