题目内容
中心在原点,对称轴为坐标轴的双曲线的渐近线方程为 ,且双曲线过点P(2,1),则双曲线的方程为________.
,且双曲线过点P(2,1),则双曲线的方程为________.

分析:由题意设双曲线方程为
 ,把点P(2,1)代入求出λ,从而得到双曲线方程.
,把点P(2,1)代入求出λ,从而得到双曲线方程.解答:由题意设双曲线方程为
 ,
,把点P(2,1)代入,得
 ,
,∴双曲线的方程为
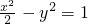 .
.答案:
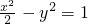 .
.点评:本题考查双曲线的性质和应用,解题时要认真审题,仔细解答,注意公式的灵活运用.

练习册系列答案
相关题目