题目内容
正整数集合Ak中的最小元素为1,最大元素为2010,并且各元素可以从小到大排列成一个公差为k的等差数列,则并集A7∪A41中的元素个数为( )
| A、300 | B、310 |
| C、330 | D、360 |
考点:并集及其运算
专题:
分析:由题意知A7通项是an=7n-6,A7有288个元素,A41通项是an=41n-40,A41有50个元素,A7∩A41有8个元素,由此能求出A7∪A41中元素个数.
解答:
解:A7里面各元素可以从小到大排列成一个公差为7的等差数列,
A7={1,8,15,…,2010},通项是an=7n-6,
a288=7×288-6=2010,
那么A7有288个元素,
A41里面各元素可以从小到大排列成一个公差为41的等差数列,
A41={1,42,83,…,2010},
通项是an=41n-40
a50=41×50-40=2010
那么A41有50个元素
令41m-40=7n-6
则n=
(41m-34),
因为41是质数
所以当m=1,8,15,22,29,36,43,50时对应的n=1,42,83,124,165,206,247,288是正整数
所以A7∩A41有8个元素,
那么A7∪A41有288+50-8=330个元素.
故选:C.
A7={1,8,15,…,2010},通项是an=7n-6,
a288=7×288-6=2010,
那么A7有288个元素,
A41里面各元素可以从小到大排列成一个公差为41的等差数列,
A41={1,42,83,…,2010},
通项是an=41n-40
a50=41×50-40=2010
那么A41有50个元素
令41m-40=7n-6
则n=
| 1 |
| 7 |
因为41是质数
所以当m=1,8,15,22,29,36,43,50时对应的n=1,42,83,124,165,206,247,288是正整数
所以A7∩A41有8个元素,
那么A7∪A41有288+50-8=330个元素.
故选:C.
点评:本题考查并集中元素个数的求法,解题时要认真审题,是基础题.

练习册系列答案
相关题目
 如图放置的几何体的俯视图为( )
如图放置的几何体的俯视图为( )A、 |
B、 |
C、 |
D、 |
函数f(x)=2sin(
x+
)是( )
| 2 |
| 3 |
| 15π |
| 2 |
| A、周期为3π的偶函数 | ||
| B、周期为3π的奇函数 | ||
C、周期为
| ||
D、周期为
|
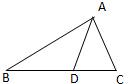 如图,已知
如图,已知| AB |
| a |
| AC |
| b |
| BD |
| DC |
| a |
| b |
| AD |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
函数f(x)=2lnx-
x2+x的图象大致是( )
| 1 |
| 2 |
A、 |
B、 |
C、 |
D、 |
如果{an}为递增数列(n∈N*),则{an}的通项公式可以为( )
| A、an=n2-n-2 | ||
| B、an=-2n+3 | ||
C、an=
| ||
| D、an=n-log2n |
已知偶函数f(x)在区间[0,4]上是增函数,则f(-3)和f(π)的大小关系是( )
| A、f(-3)>f(π) |
| B、f(-3)≥f(π) |
| C、f(-3)<f(π) |
| D、无法确定 |
函数y=
的定义域是( )
| 2cosx-1 |
A、[2kπ-
| ||||
B、[2kπ-
| ||||
C、[2kπ+
| ||||
D、[2kπ-
|