题目内容
4.求圆心在l1:y-3x=0上,与x轴相切,且被直线l2:x-y=0截得弦长为$2\sqrt{7}$的圆的方程.分析 根据题意,设圆心为C(a,3a),算出点C到直线x-y=0的距离,根据垂径定理建立方程,由于所求的圆与x轴相切,所以r2=9a2,即可得到所求圆的方程.
解答 解:由已知设圆心为(a,3a)--------(1分)
与轴相切则r=|3a|---------(2分)
圆心到直线的距离$d=\frac{{|{2a}|}}{{\sqrt{2}}}$----------(3分)
弦长为$2\sqrt{7}$得:$7+\frac{{4{a^2}}}{2}=9{a^2}$-------(4分)
解得a=±1---------(5分)
圆心为(1,3)或(-1,-3),r=3-----------(6分)
圆的方程为(x-1)2+(y-3)2=9---------(7分)
或(x+1)2+(y+3)2=9----------(8分)
点评 本题给出圆满足的条件,求圆的方程.着重考查了圆的标准方程、点到直线的距离公式、直线与圆的位置关系等知识,属于中档题.

练习册系列答案
相关题目
14.要得到函数y=sinx的图象,只需将函数$y=sin(x-\frac{π}{3})$的图象( )
| A. | 向右平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向左平移$\frac{π}{6}$个单位 |
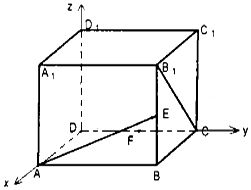 在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,
在正方体ABCD-A1B1C1D1中,如图E、F分别是BB1,CD的中点,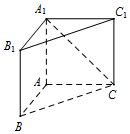 如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC=$\sqrt{2}$,则异面直线A1C与B1C1所成的角为$\frac{π}{3}$..
如图,直三棱柱ABC-A1B1C1中,侧棱AA1⊥平面ABC.若AB=AC=AA1=1,BC=$\sqrt{2}$,则异面直线A1C与B1C1所成的角为$\frac{π}{3}$..