题目内容
cos345°= .
考点:运用诱导公式化简求值
专题:计算题,三角函数的求值
分析:运用诱导公式和两角差的余弦公式,即可得到.
解答:
解:cos345°=cos(360°-15°)
=cos15°=cos(45°-30°)
=cos45°cos30°+sin45°sin30°
=
×
+
×
=
.
故答案为:
=cos15°=cos(45°-30°)
=cos45°cos30°+sin45°sin30°
=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
=
| ||||
| 4 |
故答案为:
| ||||
| 4 |
点评:本题考查诱导公式的运用:求三角函数值,考查两角差的余弦公式,考查运算能力,属于基础题.

练习册系列答案
相关题目
已知x为实数,条件p:x2<x,条件q:
>2,则p是q的( )
| 1 |
| x |
| A、充要条件 |
| B、必要不充分条 |
| C、充分不必要条件 |
| D、既不充分也不必要条件 |
已知sinα cosα=
,则sinα+cosα=( )
| 1 |
| 2 |
| A、2 | ||
| B、0 | ||
C、
| ||
D、±
|
若函数f(x)=(1+cosx)10+(1-cosx)10,x∈[0,π],则其最大值等于( )
| A、2048 | B、512 |
| C、2 | D、1024 |
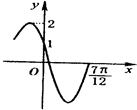
如图是函数f(x)=Asin(ωx+φ)(A>0,0<ω<3,0<φ<π)的图象的一部分,则ωφ=( )

A、
| ||
B、
| ||
C、
| ||
D、
|