题目内容
平面α∥平面β，A，C∈α，点B，D∈β，直线AB，CD相交于P，已知AP=8，BP=9，CP=16，则CD= ．
考点：平面与平面平行的性质
专题：空间位置关系与距离
分析：用面面平行的性质，可得AC∥BD，根据比例关系即可求出CD．
解答：
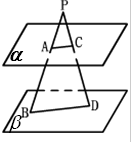
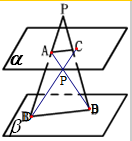解：∵平面α∥β，A，C∈α，B，D∈β，直线AB与CD交于点P，
∴AB，CD共面，且AC∥BD，
①若点P在平面α，B的外部，
∴
=
，
∵AP=8，BP=9，CP=16，
∴
=
，解得PD=18，
∴CD=PD-PC=18-16=2．
②点P在平面α，B的之间，
则
=
，即
=
，解得PD=18，
则CD=CP+PD=18+16=34，
故答案为：2或34．
解：∵平面α∥β，A，C∈α，B，D∈β，直线AB与CD交于点P，∴AB，CD共面，且AC∥BD，
①若点P在平面α，B的外部，
∴
| AP |
| BP |
| CP |
| PD |
∵AP=8，BP=9，CP=16，
∴
| 8 |
| 9 |
| 16 |
| PD |
∴CD=PD-PC=18-16=2．
②点P在平面α，B的之间，
则
| AP |
| BP |
| CP |
| PD |
| 8 |
| 9 |
| 16 |
| PD |
则CD=CP+PD=18+16=34，
故答案为：2或34．
点评：本题考查面面平行的性质，考查学生的计算能力，正确运用面面平行的性质是关键．
练习册系列答案
开心蛙状元测试卷系列答案
相关题目