题目内容
12.已知函数f(x)=lnx,则函数g(x)=f(x)-f'(x)在区间[2,e]上的最大值为1-$\frac{1}{e}$.分析 求出g′(x)=$\frac{1}{x}+\frac{1}{{x}^{2}}$,可得函数g(x)在区间[2,e]上递增,g(e)=1-$\frac{1}{e}$,即函数g(x)=f(x)-f'(x)在区间[2,e]上的最大值为1-$\frac{1}{e}$
解答 解:∵f(x)=lnx,(x>0),f′(x)=$\frac{1}{x}$,
∴g(x)=lnx-$\frac{1}{x}$,则g′(x)=$\frac{1}{x}+\frac{1}{{x}^{2}}$,
在区间[2,e]上g′(x)>0恒成立,即函数g(x)在区间[2,e]上递增,g(e)=1-$\frac{1}{e}$
∴函数g(x)=f(x)-f'(x)在区间[2,e]上的最大值为1-$\frac{1}{e}$
故答案为:1-$\frac{1}{e}$
点评 本题考查了利用导数求函数最值,属于中档题.

练习册系列答案
相关题目
3.某机械厂组装A,B两种类型机械,每组装1台A或B所需要的配件材料费和工人数如下表所示.
已知该机械厂现有工人32人,可用资金55万元,组装1台A类型机械可获纯利润4万元,组装1台B类型机械可获纯利润2万元,设该机械厂计划组装A,B两种类型机械分别为x台,y台.
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问该机械厂分别组装A,B两种类型机械各多少台,才能获得最大利润?并求出此最大纯利润.
| 类型 条件 | A | B |
| 配件材料费(万元) | 20 | 5 |
| 工人数(人) | 4 | 8 |
(Ⅰ)用x,y列出满足生产条件的数学关系式,并画出相应的平面区域;
(Ⅱ)问该机械厂分别组装A,B两种类型机械各多少台,才能获得最大利润?并求出此最大纯利润.
7.若全集U=R,集合A={x|1<2x<4},B={x|x-1≥0},则A∩(∁UB)( )
| A. | {x|1<x<2} | B. | {x|0<x<1} | C. | {x|0<x≤1} | D. | {x|1≤x<2} |
5.等边△ABC在椭圆内,A是椭圆中心,B是椭圆的一个焦点,则该椭圆离心率的取值范围是( )
| A. | (0,$\sqrt{3}$-1) | B. | ($\sqrt{3}$-1,1) | C. | (0,$\frac{\sqrt{2}}{2}$) | D. | $\frac{\sqrt{2}}{2}$,1) |
9.在△ABC中,a,b,c分别是角A,B,C的对边,若(b-$\frac{6}{5}$c)sinB+csinC=asinA,则sinA=( )
| A. | $-\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | $-\frac{3}{5}$ | D. | $\frac{3}{5}$ |
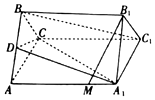 如图,在正三棱柱ABC-A1B1C1中,点D是AB的上一点,且AD=tAB.
如图,在正三棱柱ABC-A1B1C1中,点D是AB的上一点,且AD=tAB.