题目内容
15.若x∈[-$\frac{π}{6}$,$\frac{π}{4}$],则f(x)=$\frac{3si{n}^{2}x-2}{sinxcosx+co{s}^{2}{x}^{\;}}$的最大值为-$\frac{1}{2}$.分析 由三角函数公式化简可得f(x)=tanx+1-2-$\frac{1}{tanx+1}$,由x∈[-$\frac{π}{6}$,$\frac{π}{4}$]和函数的单调性可得.
解答 解:化简可得f(x)=$\frac{3si{n}^{2}x-2}{sinxcosx+co{s}^{2}{x}^{\;}}$
=$\frac{3si{n}^{2}x-2si{n}^{2}x-2co{s}^{2}x}{sinxcosx+co{s}^{2}x}$=$\frac{si{n}^{2}x-2co{s}^{2}x}{sinxcosx+co{s}^{2}x}$
=$\frac{ta{n}^{2}x-2}{tanx+1}$=$\frac{(tanx+1)^{2}-2(tanx+1)-1}{tanx+1}$
=tanx+1-2-$\frac{1}{tanx+1}$
∵x∈[-$\frac{π}{6}$,$\frac{π}{4}$],∴tanx∈[-$\frac{\sqrt{3}}{3}$,1],
∴函数f(x)=tanx+1-2-$\frac{1}{tanx+1}$为增函数,
∴最大值为1+1-2-$\frac{1}{2}$=-$\frac{1}{2}$,
故答案为:-$\frac{1}{2}$.
点评 本题考查三角函数的最值,涉及弦化切的思想和函数的单调性,属中档题.

练习册系列答案
相关题目
5.在△ABC中,内角A,B,C的对边分别为a,b,c,且acosB=bcosA,a2+b2=c2+ab,则△ABC是( )
| A. | 钝角三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 等边三角形 |
6.已知f(x)=1+x-sinx,则f(2),f(3),f(π)的大小关系正确的是( )
| A. | f(2)>f(3)>f(π) | B. | f(3)>f(2)>f(π) | C. | f(2)>f(π)>f(3) | D. | f(π)>f(3)>f(2) |
20.设f(x)为奇函数,且在(0,+∞)上是增函数,f(-2015)=0,则xf(x)>0的解集为( )
| A. | (-∞,2015)∪(2015,+∞) | B. | (-∞,-2015)∪(0,2015) | C. | (-2015,0)∪(0,2015) | D. | (-2015,0)∪(2015,+∞) |
4.两定点F1(-3,0),F2(3,0),P为曲线$\frac{|x|}{5}+\frac{|y|}{4}$=1上任意一点,则( )
| A. | |PF1|+|PF2|≥10 | B. | |PF1|+|PF2|≤10 | C. | |PF1|+|PF2|>10 | D. | |PF1|+|PF2|<10 |
5.已知函数f(x)=log2(2x+m)的定义域为(2,+∞),则f(10)等于( )
| A. | 3+log23 | B. | 3 | C. | 1+2log23 | D. | 4 |
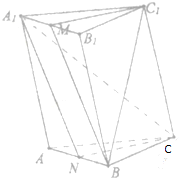 在三棱柱ABC-A1B1C1中,上下两个底面平行,侧面是平行四边形,N是AB的中点,M是A1B1的中点,求证:平面A1NC∥平面BMC1.
在三棱柱ABC-A1B1C1中,上下两个底面平行,侧面是平行四边形,N是AB的中点,M是A1B1的中点,求证:平面A1NC∥平面BMC1.