Question

给出以下三个命题：
①已知P（m，4）是椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）上的一点，F₁、F₂是左、右两个焦点，若△PF₁F₂的内切圆的半径为

3

2

，则此椭圆的离心率e=

4

5

；
②过双曲线C：

x2

a2

-

y2

b2

=1（a＞0，b＞0）的右焦点F作斜率为

3

的直线交C于A，B两点，若

AF

=4

FB

，则该双曲线的离心率e=

6

5

；
③已知F₁（-2，0）、F₂（2，0），P是直线x=-1上一动点，若以F₁、F₂为焦点且过点P的双曲线的离心率为e，则e的取值范围是[2，+∞）．
其中真命题的个数为（　　）

• A、3个
• B、2个
• C、1个
• D、0个

Answer 1

考点：命题的真假判断与应用,双曲线的简单性质

专题：阅读型,圆锥曲线的定义、性质与方程

分析：①由椭圆的定义和离心率公式，结合等积方法，即可求出；
②运用双曲线的第二定义，结合直角三角形的30°所对边的性质，及离心率公式，即可得到；
③P在x轴上时，双曲线上点到左焦点距离最小，得到a≤1，由离心率公式即可得到e的范围．

解答： 解：①∵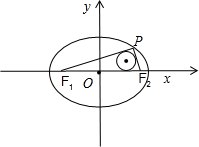△PF₁F₂的内切圆的半径为

3

2

，|PF₁|+|PF₂|=2a，|F₁F₂|=2c
∴利用三角形的面积计算公式可得：

1

2

（2a+2c）×

3

2

=

1

2

×2c×4，
3a=5c，e=

c

a

=

3

5

，故①错误；
②设双曲线的右准线为l：x=

a2

c

，A到直线l的距离为d₁，B到直线l的距离为d₂，由双曲线的第二定义得到：
e=

AF

d1

=

BF

d2

=

AF-BF

d1-d2

，由

AF

=4

FB

，设BF=t，则AF=4t，由直角三角形中，30°所对的直角边是斜边的一半，得d₁-d₂=

5t

2

，则e=

3t

5t 2

=

6

5

．故②正确；
③P在x轴上时，双曲线上点到左焦点距离最小，∴c-a≥1，∴2-a≥1，
∴a≤1，e=

c

a

=

2

a

又a≤1，∴e≥2，故③正确．
故选：B．

点评：本题考查圆锥曲线的定义、方程和性质，特别是离心率的取值，考查运算能力和判断能力，属于中档题．