题目内容
17.等比数列{an}的前n项和为Sn,若S14=3S7=3,则S28=( )| A. | 9 | B. | 15 | C. | 8 | D. | 12 |
分析 由已知得S7=1,S14=3,由等比列的性质得S7,S14-S7,S21-S14,S28-S21构成以1为首项,以2为公比的等比数列,由此能求出S28的值.
解答 解:∵等比数列{an}的前n项和为Sn,S14=3S7=3,
∴S7=1,S14=3,
由等比列的性质得S7,S14-S7,S21-S14,S28-S21构成以1为首项,以2为公比的等比数列,
∴S21-S14=4,解得S21=4+3=7,
S28-S21=8,解得S28=8+7=15.
故选:B.
点评 本题考查等比数列的前28项和的求法,考查等比数列的性质等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是基础题.

练习册系列答案
相关题目
8.下列四个数中最大的是( )
| A. | (ln2)2 | B. | ln(ln2) | C. | ln$\sqrt{2}$ | D. | ln2 |
5.设向量$\overrightarrow a=({1,x})$,$\overrightarrow b=({f(x),-x})$且$\overrightarrow a•\overrightarrow b=g(x)$,x∈R,若函数f(x)为偶函数,则g(x)的解析式可以为( )
| A. | x3 | B. | 1+x | C. | cosx | D. | xex |
12.下列说法中正确的是( )
| A. | 有两个面平行,其余各面都是三角形的几何体叫棱柱 | |
| B. | 有两个面平行,其余各面都是梯形的几何体叫棱台 | |
| C. | 有一个面是多边形,其余各面都是五边形的几何体叫棱锥 | |
| D. | 棱台各侧棱的延长线交于一点 |
6.若正数x,y满足$\frac{3}{x}+\frac{1}{y}=1$,则3x+4y的最小值是( )
| A. | 24 | B. | 28 | C. | 30 | D. | 25 |
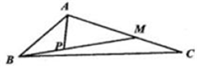 如图,已知△ABC中,点M在线段AC上,点P在线段BM上,且满足$\frac{AM}{MC}$=$\frac{MP}{PB}$=2,若|${\overrightarrow{AB}}$|=2,|${\overrightarrow{AC}}$|=3,∠BAC=120°,则$\overrightarrow{AP}$•$\overrightarrow{BC}$的值为-2.
如图,已知△ABC中,点M在线段AC上,点P在线段BM上,且满足$\frac{AM}{MC}$=$\frac{MP}{PB}$=2,若|${\overrightarrow{AB}}$|=2,|${\overrightarrow{AC}}$|=3,∠BAC=120°,则$\overrightarrow{AP}$•$\overrightarrow{BC}$的值为-2.