题目内容
5．
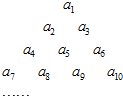设数列{an}按三角形进行排列，如图，第一层一个数a1，第二层两个数a2和a3，第三层三个数a4，a5和a6，以此类推，且每个数字等于下一层的左右两个数字之和，如a1=a2+a3，a2=a4+a5，a3=a5+a6，…．（1）若第四层四个数为0或1，a1为奇数，则第四层四个数共有多少种不同取法？
（2）若第十一层十一个数为0或1，a1为5的倍数，则第十一层十一个数共有多少种不同取法？
分析 （1）若第四层四个数为0或1，则a1=a7+3a8+3a9+a10，由a1为奇数，进而得到答案；
（2）若第十一层十一个数为0或1，a1为5的倍数，则若a1为5的倍数，则a56，a66均为0，a57，a58，a65任意，进而得到答案．
解答 解：（1）若第四层四个数为0或1，则a1=a7+3a8+3a9+a10，
则a7，a8，a9，a10中有一个1，或有三个1，
若a7，a8，a9，a10中有一个1，则有4种情况；
若a7，a8，a9，a10中有三个1，则有4种情况；
共8种情况；
（2）根据（1）中结论，若第十一层十一个数为0或1，
则a1=a56+10（a57+a58+…+a65）+a66，
若a1为5的倍数，则a56，a66均为0，
a57，a58，a65任意，
则第十一层十一个数共有29=512种不同取法．
点评 归纳推理的一般步骤是：（1）通过观察个别情况发现某些相同性质；（2）从已知的相同性质中推出一个明确表达的一般性命题（猜想）．
练习册系列答案
阅读快车系列答案
相关题目
15．sin20°cos10°+cos20°sin10°=（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $-\frac{1}{2}$ | D． | $-\frac{{\sqrt{3}}}{2}$ |
20．已知不等式2x+m+$\frac{8}{x-1}$＞0对一切x∈（1，+∞）恒成立，则实数m的取值范围是（ ）
| A． | m＞-10 | B． | m＜-10 | C． | m＞-8 | D． | m＜-8 |
10．已知α是第二象限的角，其终边上的一点为$P（x，\sqrt{5}）$，且$cosα=\frac{{\sqrt{2}}}{4}x$，则tanα=（ ）
| A． | $\frac{{\sqrt{15}}}{5}$ | B． | $\frac{{\sqrt{15}}}{3}$ | C． | $-\frac{{\sqrt{15}}}{5}$ | D． | $-\frac{{\sqrt{15}}}{3}$ |
14．已知f（x）=（4-m）x2-4x+1，a为正整数，满足f（a）＜0的a的个数有且仅有两个，则实数m的取值范围为（ ）
| A． | 2＜m≤3 | B． | $\frac{9}{4}＜m≤\frac{25}{9}$ | C． | m$＞\frac{25}{9}$ | D． | m$≤\frac{9}{4}$ |