题目内容
10.已知α是第二象限的角,其终边上的一点为$P(x,\sqrt{5})$,且$cosα=\frac{{\sqrt{2}}}{4}x$,则tanα=( )| A. | $\frac{{\sqrt{15}}}{5}$ | B. | $\frac{{\sqrt{15}}}{3}$ | C. | $-\frac{{\sqrt{15}}}{5}$ | D. | $-\frac{{\sqrt{15}}}{3}$ |
分析 由已知得cosα=$\frac{x}{\sqrt{{x}^{2}+5}}$=$\frac{\sqrt{2}}{4}x$,且x<0,从而x=-$\sqrt{3}$,由此能求出tanα.
解答 解:∵α是第二象限的角,其终边上的一点为$P(x,\sqrt{5})$,
且$cosα=\frac{{\sqrt{2}}}{4}x$,
∴cosα=$\frac{x}{\sqrt{{x}^{2}+5}}$=$\frac{\sqrt{2}}{4}x$,且x<0,
解得x=-$\sqrt{3}$,
∴tanα=$\frac{\sqrt{5}}{-\sqrt{3}}$=-$\frac{\sqrt{15}}{3}$.
故选:D.
点评 本题考查任意角三角函数值的求法,是基础题,解题时要认真审题,注意三角函数性质的合理运用.

练习册系列答案
相关题目
1.函数f(x)=$\left\{\begin{array}{l}{|lnx|-1,x>0}\\{-{x}^{2}+2x+3,x≤0}\end{array}\right.$的零点个数为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
18.已知函数f(x)=x2-2ax+5(a>1),g(x)=log3x.若函数f(x)的定义域与值域均为[1,a],且对于任意的x1,x2∈[1,a+1],$|{f({x_1})-g({x_2})}|≤{4^t}+{2^t}$恒成立,则满足条件的实数t的取值范围是( )
| A. | [-2,8] | B. | [0,8] | C. | [0,+∞) | D. | [0,8) |
19.“α=$\frac{π}{2}$”是sin(α-β)=cosβ“的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
20.已知数列{an}满足a1=8,2an+1-an=4,则a12的值为( )
| A. | $\frac{257}{128}$ | B. | $\frac{513}{256}$ | C. | $\frac{2049}{512}$ | D. | $\frac{2049}{1024}$ |
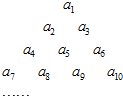 设数列{an}按三角形进行排列,如图,第一层一个数a1,第二层两个数a2和a3,第三层三个数a4,a5和a6,以此类推,且每个数字等于下一层的左右两个数字之和,如a1=a2+a3,a2=a4+a5,a3=a5+a6,….
设数列{an}按三角形进行排列,如图,第一层一个数a1,第二层两个数a2和a3,第三层三个数a4,a5和a6,以此类推,且每个数字等于下一层的左右两个数字之和,如a1=a2+a3,a2=a4+a5,a3=a5+a6,….