Question

5．在△ABC中，已知|$\overrightarrow{AB}$|=3，|$\overrightarrow{AC}$|=2，∠BAC=120°，D在BC上，且$\overrightarrow{BD}$=$\frac{1}{4}$$\overrightarrow{BC}$，计算$\overrightarrow{AD}$•$\overrightarrow{BC}$．

Answer 1

分析 根据向量加法及减法的几何意义，便可用$\overrightarrow{AB}，\overrightarrow{AC}$分别表示$\overrightarrow{AD}，\overrightarrow{BC}$，从而得到$\overrightarrow{AD}•\overrightarrow{BC}=（\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}）•（\overrightarrow{AC}-\overrightarrow{AB}）$，然后根据条件进行数量积的计算即可．

解答 解：如图，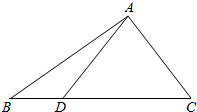

$\overrightarrow{AD}=\overrightarrow{AB}+\overrightarrow{BD}=\overrightarrow{AB}+\frac{1}{4}\overrightarrow{BC}$=$\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$；
∴$\overrightarrow{AD}•\overrightarrow{BC}=（\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}）•（\overrightarrow{AC}-\overrightarrow{AB}）$=$\frac{1}{2}\overrightarrow{AB}•\overrightarrow{AC}-\frac{3}{4}{\overrightarrow{AB}}^{2}+\frac{1}{4}{\overrightarrow{AC}}^{2}$=$-\frac{3}{2}-\frac{27}{4}+1=-\frac{29}{4}$．

点评 考查向量加法、减法的几何意义，向量的数乘运算，以及数量积的运算及其计算公式．