题目内容
12.若抛物线y=2x2上两点A(x1,y1)、B(x2,y2)关于直线y=x+$\frac{3}{2}$对称,则x1•x2=( )| A. | $\frac{5}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -3 |
分析 先利用条件得出A、B两点连线的斜率k,再利用A、B两点的中点在直线y=x+$\frac{3}{2}$,与已知条件联立求出x1•x2的值.
解答 解:由条件得A(x1,y1)、B(x2,y2)两点连线的斜率k=-1,
而y2-y1=2(x22-x12) ①,得x2+x1=-$\frac{1}{2}$ ②,且($\frac{{x}_{2}+{x}_{1}}{2}$,$\frac{{y}_{2}+{y}_{1}}{2}$)在直线y=x+$\frac{3}{2}$上,
即$\frac{{y}_{2}+{y}_{1}}{2}$=$\frac{{x}_{2}+{x}_{1}}{2}$+$\frac{3}{2}$,即y2+y1=x2+x1+3 ③
又因为A(x1,y1)、B(x2,y2)两点在抛物线y=2x2上,
所以有2(x22+x12)=x2+x1+3,即2[(x2+x1)2-2x2x1]=x2+x1+3 ④,
把①②代入④整理解得x1•x2=-$\frac{1}{2}$
故选:C.
点评 本题是对直线与抛物线位置关系以及点与直线位置的综合考查.当两点关于已知直线对称时,有两条结论,一是两点的中点在已知直线上;二是两点的连线与已知直线垂直.

练习册系列答案
相关题目
4.不等式log0.3(x2-3x-4)-log0.3(2x+10)>0的解集是( )
| A. | (-2,-1) | B. | (4,7) | C. | (-2,-1)∪(4,7) | D. | ∅ |
10.某校在对学生是否喜欢数学的抽样调查中,随机抽取了300名学生,相关的数据如表所示:
由表中数据直观分析,该校学生的性别与是否喜欢数学之间有关系(填“有”或“无”).
| 喜欢数学课程 | 不喜欢数学课程 | 总计 | |
| 男 | 37 | 85 | 122 |
| 女 | 35 | 143 | 178 |
| 总计 | 72 | 228 | 300 |
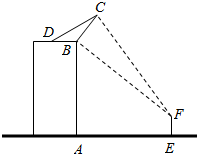 如图,一楼房高AB为19$\sqrt{3}$米,某广告公司在楼顶安装一块宽BC为4米的广告牌,CD为拉杆,广告牌的倾角为60°,安装过程中,一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设AE=x米,该监理人员观察广告牌的视角∠BFC=θ.
如图,一楼房高AB为19$\sqrt{3}$米,某广告公司在楼顶安装一块宽BC为4米的广告牌,CD为拉杆,广告牌的倾角为60°,安装过程中,一身高为$\sqrt{3}$米的监理人员EF站在楼前观察该广传牌的安装效果:为保证安全,该监理人员不得站在广告牌的正下方:设AE=x米,该监理人员观察广告牌的视角∠BFC=θ.