题目内容
17.已知圆C:x2+(y-1)2=5,直线1过定点P(1,1).(1)求圆心C到直线1距离最大时的直线1的方程;
(2)若1与圆C交与不同两点A、B,求弦AB的中点M的轨迹方程.
分析 (1)由定点P(1,1)在圆C:x2+(y-1)2=5的内部,结合圆的弦长、弦心距及半径的关系可得圆心C到直线1距离最大时的直线1的方程;
(2)设AB中点M(x,y),当AB斜率存在时,由KAB•KCM=-1,化简可得AB中点M的轨迹方程;当AB的斜率不存在时,点M的坐标也满足此轨迹方程,从而得出结论.
解答 解:(1)定点P(1,1)在圆C:x2+(y-1)2=5的内部,
圆心C到直线1距离最大时的直线1与CP垂直,
∵${k}_{CP}=\frac{1-1}{1-0}=0$,∴所求直线l的斜率不存在,
则直线方程为x=1;
(2)设AB中点M(x,y),当AB的斜率存在时,由题意可得CM⊥AB,故有KAB•KCM=-1.
∴$\frac{y-1}{x-1}•\frac{y-1}{x-0}=-1$,化简可得$(x-\frac{1}{2})^{2}+(y-1)^{2}=\frac{1}{4}$,
当AB的斜率不存在时,直线AB的方程为x=1,此时AB的中点M的坐标为(1,1),
也满足$(x-\frac{1}{2})^{2}+(y-1)^{2}=\frac{1}{4}$.
综上可得,AB中点M的轨迹方程为$(x-\frac{1}{2})^{2}+(y-1)^{2}=\frac{1}{4}$.
点评 本题主要考查直线和圆的位置关系的判定,直线过定点问题,求点的轨迹方程,属于中档题

练习册系列答案
相关题目
12.若抛物线y=2x2上两点A(x1,y1)、B(x2,y2)关于直线y=x+$\frac{3}{2}$对称,则x1•x2=( )
| A. | $\frac{5}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -3 |
9.在等比数列{an}中,Sn是其前n项和,已知a3=2S2+1,a4=2S3+1,则S4=( )
| A. | 4 | B. | 16 | C. | 20 | D. | 40 |
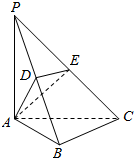 在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°,若AD⊥PB,垂足为D,AE⊥PC,垂足为E,求证:AD⊥PC.
在三棱锥P-ABC中,PA⊥面ABC,∠ABC=90°,若AD⊥PB,垂足为D,AE⊥PC,垂足为E,求证:AD⊥PC.