题目内容
1.已知向量$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-1,0),若(λ$\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$,则实数λ的值为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 由$\overrightarrow{a}$,$\overrightarrow{b}$的坐标求出(λ$\overrightarrow{a}$+$\overrightarrow{b}$)的坐标,然后利用向量垂直的坐标表示求得实数λ的值.
解答 解:∵$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(-1,0),
∴λ$\overrightarrow{a}$+$\overrightarrow{b}$=λ(1,2)+(-1,0)=(λ-1,2λ),
由(λ$\overrightarrow{a}$+$\overrightarrow{b}$)⊥$\overrightarrow{b}$,得λ-1=0,∴λ=1.
故选:B.
点评 本题考查平面向量的坐标运算,考查两向量垂直的坐标表示,是基础的计算题.

练习册系列答案
相关题目
12.若抛物线y=2x2上两点A(x1,y1)、B(x2,y2)关于直线y=x+$\frac{3}{2}$对称,则x1•x2=( )
| A. | $\frac{5}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -3 |
9.在等比数列{an}中,Sn是其前n项和,已知a3=2S2+1,a4=2S3+1,则S4=( )
| A. | 4 | B. | 16 | C. | 20 | D. | 40 |
18.已知角α的顶点与原点O重合,始边与x轴的正半轴重合,若它的终边经过点P(2,3),则$tan({2α+\frac{π}{4}})$=( )
| A. | $-\frac{7}{17}$ | B. | $\frac{17}{7}$ | C. | $-\frac{12}{5}$ | D. | $\frac{5}{12}$ |
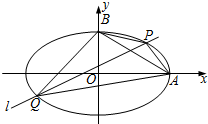 已知平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点和上顶点分别为A,B,椭圆的离心率为$\frac{\sqrt{3}}{2}$,且过点(1,$\frac{\sqrt{3}}{2}$).
已知平面直角坐标系xOy中,已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点和上顶点分别为A,B,椭圆的离心率为$\frac{\sqrt{3}}{2}$,且过点(1,$\frac{\sqrt{3}}{2}$).