题目内容
3.已知函数f(x)=x3+bx2+cx+d的图象过点P(0,2),且在点M(-1,f(-1))处的切线方程为6x-y+7=0,求(1)函数y=f(x)的解析式;
(2)方程f(x)=0的零点个数.
分析 (1)求函数的导数,根据条件建立方程组关系即可得到结论;
(2)确定函数的单调性,极大值,即可求出方程f(x)=0的零点个数.
解答 解:(1)∵函数f(x)=x3+bx2+cx+d图象经过(0,2)点,
∴f(0)=2得d=2,
∵在x=-1处的切线为6x-y+7=0,
∴解得y=1,即 切点(-1,1)代入f(x)中得-1+b-c+2=1,即b=c,
切线斜率k=6,即f′(-1)=6,
函数的导数为f′(x)=3x2+2bx+c,即f′(-1)=3-2b+c=6,
解得b=c=-3,
则f(x)=x3-3x2-3x+2.
(2)f(x)=x3-3x2-3x+2=0,
∴f′(x)=3x2-6x-3
当f′(x)=0时,3x2-6x-3=0
∴x2-2x-1=0
∴(x-1)2=2
∴x=1±$\sqrt{2}$
令f′(x)>0,得x<1-$\sqrt{2}$或x$>1+\sqrt{2}$
令f′(x)<0,得1-$\sqrt{2}$<x<1-$\sqrt{2}$,
∴函数的单调增区间为(-∞,1-$\sqrt{2}$),(1+$\sqrt{2}$,+∞),函数的单调减区间为(1-$\sqrt{2}$,1+$\sqrt{2}$).
∵f(1-$\sqrt{2}$)=-3+4$\sqrt{2}$<0,∴方程f(x)=0的零点个数为1.
点评 本题主要考查函数解析式的求解,考查函数的零点,求函数的导数,利用导数的几何意义、单调性是解决本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
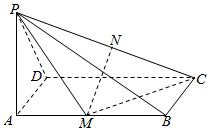 如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD,M为AB的中点.
如图,四棱锥P-ABCD的底面为矩形,PA⊥底面ABCD,且PA=AD,M为AB的中点.