题目内容
已知函数f(x)＝mx3＋nx2的图象在点(－1,2)处的切线恰好与直线3x＋y＝0平行，若f(x)在区间[t，t＋1]上单调递减，则实数t的取值范围是________．
[－2，－1]
[解析] 由题意知，点(－1,2)在函数f(x)的图象上，故－m＋n＝2①
又f ′(x)＝3mx2＋2nx，由条件知f ′(－1)＝－3，
故3m－2n＝－3②
联立①②解得：m＝1，n＝3，即f(x)＝x3＋3x2，
令f ′(x)＝3x2＋6x≤0，解得－2≤x≤0，
则[t，t＋1]⊆[－2,0]，故t≥－2且t＋1≤0，
所以t∈[－2，－1]．
练习册系列答案
相关题目
＋
B.
＋
＋
D．n2＋n
x＋φ)(0<φ<π)，若f(x)＋f ′(x)为奇函数，则φ＝________.
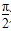)上不是凸函数的是________(把你认为正确的序号都填上)．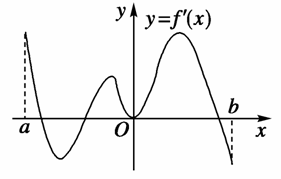
(m∈R)在区间[1，e]上取得最小值4，则m＝________.
R D.
R
,
,若
,则
的值为
D． 0或1