题目内容
设α,β为两个不重合的平面,m,n是两条不重合的直线,则下列四个命题中是真命题的是( )
| A、若m⊥n,m⊥α,则n∥α |
| B、若n?α,m?β,α与β相交且不垂直,则n与m不垂直 |
| C、若α⊥β,α∩β=m,m⊥n,则n⊥β |
| D、若m∥n,n⊥α,α∥β,则m⊥β |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:根据线面垂直的性质与线面平行的判定,可得A是假命题;若n?α,m?β,α与β相交且不垂直,则n与m不垂直,由线线的位置关系判断B不正确;C可由面面垂直的性质判断;D由线面垂直的条件判断.
解答:
解:对于A,因为m⊥α,m⊥n,则n∥α或n?α,不一定得到n∥α,故A是假命题;
对于B,若n?α,m?β,α与β相交且不垂直,则n与m不垂直,是错误命题,因为两个不垂直的平面中也存在互相垂直的两条直线;
对于C,由面面垂直的性质定理,n?α,则n与β不垂直,故C错;
对于D,m∥n,n⊥α,则m⊥α,又α∥β,所以,m⊥β,故D正确;
故选:D.
对于B,若n?α,m?β,α与β相交且不垂直,则n与m不垂直,是错误命题,因为两个不垂直的平面中也存在互相垂直的两条直线;
对于C,由面面垂直的性质定理,n?α,则n与β不垂直,故C错;
对于D,m∥n,n⊥α,则m⊥α,又α∥β,所以,m⊥β,故D正确;
故选:D.
点评:本题考查空间线面位置关系,考查学生分析解决问题的能力.

练习册系列答案
相关题目
在空间直角坐标系中,点B是点A(2,-3,5)关于xOy面的对称点,则|AB|=( )
| A、10 | ||
B、
| ||
C、
| ||
| D、38 |
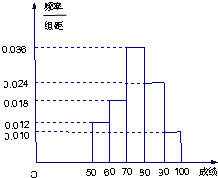 某年级n名学生的一次数学质量测验成绩的频率分布直方图如图所示,成绩不低于70分的学生人数有168人,则n为( )
某年级n名学生的一次数学质量测验成绩的频率分布直方图如图所示,成绩不低于70分的学生人数有168人,则n为( )| A、240 | B、560 |
| C、280 | D、420 |
已知锐角三角形的边长分别是3,5,x,则x的取值范围是( )
A、1<x<
| ||
B、4<x<
| ||
| C、1<x<4 | ||
D、4<x<
|
在△ABC中,若A=30°,B=60°,b=
,则a等于( )
| 3 |
| A、3 | ||
| B、1 | ||
| C、2 | ||
D、
|