题目内容
6.已知直线l经过两点A(2,1),B(6,3).(1)求直线l的方程;(请用一般式作答)
(2)圆C的圆心为直线l与直线x-y-1=0的交点,且圆C与x轴相切,求圆C的标准方程.
分析 (1)直线l经过两点A(2,1),B(6,3),利用两点式,即可求直线l的方程;
(2)求出圆心坐标,利用圆C与x轴相切,求圆C的标准方程.
解答 解:(1)∵直线l经过两点A(2,1),B(6,3),
∴直线l的方程为$\frac{y-1}{3-1}=\frac{x-2}{6-2}$,即x-2y=0;
(2)由$\left\{\begin{array}{l}{x-2y=0}\\{x-y-1=0}\end{array}\right.$,可得x=2,y=1,
∴圆心为(2,1)
∵圆C与x轴相切,
∴圆C的标准方程为(x-2)2+(y-1)2=1.
点评 本题考查直线与圆的方程,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
18.($\frac{1}{2}$x-1)(2x-$\frac{1}{x}$)6的展开式中x的系数为( )
| A. | 40 | B. | -80 | C. | 120 | D. | -160 |
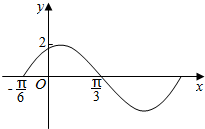 函数y=f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.
函数y=f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.