题目内容
17.已知函数f(x)=log2(2x2-4x+10),g(x)=f(x)-log2(x2+x+1)(1)求函数f(x)的值域;
(2)若g(x)>1,求x的取值范围.
分析 (1)先对函数的真数配方,求得真数的最小值,从而求得函数的最小值,即得值域;
(2)将不等式等价为:$\frac{2x^2-4x+10}{x^2+x+1}$>2,解之即可.
解答 解:(1)f(x)=log2[2(x-1)2+8],
显然,当x=1时,真数取得最小值8,
所以,函数的最小值为log28=3,
即f(x)min=f(1)=log28=3,
因此,函数f(x)的值域为[3,+∞);
(2)g(x)=f(x)-log2(x2+x+1)
=log2(2x2-4x+10)-log2(x2+x+1)
=log2$\frac{2x^2-4x+10}{x^2+x+1}$>1,
所以,$\frac{2x^2-4x+10}{x^2+x+1}$>2,
解得x<$\frac{4}{3}$,
即x的取值范围为(-∞,$\frac{4}{3}$).
点评 本题主要考查了对数函数的图象与性质,涉及函数的单调性和最值,以及对数的运算性质和不等式的解法,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知程序框图如图所示.
已知程序框图如图所示.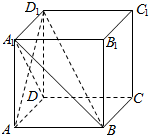 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中. 设数列{xn}的各项都为正数且x1=1.如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,若(2xn+1)$\overrightarrow{{P}_{n}C}$+$\overrightarrow{{P}_{n}A}$=$\frac{1}{3}$xn+1$\overrightarrow{{P}_{n}B}$,则x5的值为31.
设数列{xn}的各项都为正数且x1=1.如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,若(2xn+1)$\overrightarrow{{P}_{n}C}$+$\overrightarrow{{P}_{n}A}$=$\frac{1}{3}$xn+1$\overrightarrow{{P}_{n}B}$,则x5的值为31.