题目内容
15.在△ABC中,5sinA+12cosB=15,12sinB+5cosA=2,则∠C=30度.分析 先对条件中两个式子平方后相加得到关于A+B的正弦值,再由诱导公式得到角C的正弦值,最后得到答案.
解答 解:对5sinA+12cosB=15,12sinB+5cosA=2,
两个方程两边同时平方,然后两式相加:25(sin2A+cos2A)+120(sinAcosB+sinBcosA)+144(sin2B+cos2B)=229.
化简得:120(sinAcosB+sinBcosA)=60.
∴sin(A+B)=$\frac{1}{2}$
∴sin(180°-C)=sinC=$\frac{1}{2}$
得出∠C=$\frac{π}{6}$或$\frac{5π}{6}$,
若C=$\frac{5π}{6}$,则A+B=$\frac{π}{6}$,cosB<1,2sinA<1,4sinA+2cosB=1,不成立,
所以C=$\frac{π}{6}$=30°.
故答案为:30.
点评 本题主要考查同角三角函数的基本关系和两角和与差的正弦公式的应用.属中档题.

练习册系列答案
相关题目
4.动圆P与直线l:x=-1相切,且与圆(x-2)2+y=1相外切,设动圆C的圆心的轨迹为C,过点(8,0)的直线m与C相交于A、B两点.
(1)求轨迹C的方程;
(2)设O为坐标原点,求证:OA⊥OB.
(1)求轨迹C的方程;
(2)设O为坐标原点,求证:OA⊥OB.
5.已知sin($\frac{π}{2}$-θ)-cos(π+θ)=3sin(2π-θ),则sinθcosθ+cos2θ等于( )
| A. | $\frac{3}{13}$ | B. | $\frac{2}{5}$ | C. | -$\frac{3}{5}$ | D. | -$\frac{2}{5}$ |
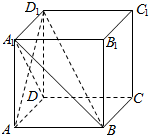 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.