题目内容
1.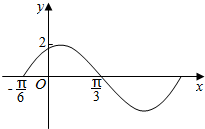 函数y=f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.
函数y=f1(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的一段图象如图所示.(1)求函数f1(x)的解析式;
(2)将函数y=f1(x)的图象向右平移$\frac{π}{4}$个单位长度,得到函数图y=f2(x)的图象,求y=f2(x)的最大值,并求出此时自变量x的取值范围.
分析 (1)由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,从而得到函数的解析式.
(2)利用函数y=Asin(ωx+φ)的图象变换,可求得y=f2(x)=f1(x-$\frac{π}{4}$)=2sin(2x-$\frac{π}{6}$),从而可求y=f2(x)的最大值及取最大值时的自变量的值.
解答 解:(1)由函数的图象可得,A=2,由 $\frac{1}{2}•\frac{2π}{ω}$=$\frac{π}{3}-(-\frac{π}{6})$,解得ω=2.
再由点($\frac{π}{3}$,0)在函数图象上,可得 2×$\frac{π}{3}$+φ=kπ,k∈Z,解得φ=kπ-$\frac{2π}{3}$,k∈Z,
又|φ|<$\frac{π}{2}$,可得:φ=$\frac{π}{3}$.
故函数的解析式为f1(x)=2sin(2x+$\frac{π}{3}$).
(2)将函数y=f1(x)的图象向右平移$\frac{π}{4}$个单位长度,
得到函数图y=f2(x)=2sin[2(x-$\frac{π}{4}$)+$\frac{π}{3}$]=2sin(2x-$\frac{π}{6}$).
y=f2(x)的最大值为2,此时2x-$\frac{π}{6}$=2kπ+$\frac{π}{2}$,k∈Z,解得:x=kπ+$\frac{π}{3}$,k∈Z.
点评 本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,考查函数y=Asin(ωx+φ)的图象变换,考查正弦函数的最值,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 设数列{xn}的各项都为正数且x1=1.如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,若(2xn+1)$\overrightarrow{{P}_{n}C}$+$\overrightarrow{{P}_{n}A}$=$\frac{1}{3}$xn+1$\overrightarrow{{P}_{n}B}$,则x5的值为31.
设数列{xn}的各项都为正数且x1=1.如图,△ABC所在平面上的点Pn(n∈N*)均满足△PnAB与△PnAC的面积比为3:1,若(2xn+1)$\overrightarrow{{P}_{n}C}$+$\overrightarrow{{P}_{n}A}$=$\frac{1}{3}$xn+1$\overrightarrow{{P}_{n}B}$,则x5的值为31.