题目内容
15.复数z满足iz=|1-i|,则z的虚部为$-\sqrt{2}$.分析 由iz=|1-i|,得$z=\frac{|1-i|}{i}$,然后利用复数代数形式的乘除运算化简复数z得答案.
解答 解:由iz=|1-i|,
得$z=\frac{|1-i|}{i}$=$\frac{-\sqrt{2}i}{-{i}^{2}}=-\sqrt{2}i$,
则z的虚部为:$-\sqrt{2}$.
故答案为:$-\sqrt{2}$.
点评 本题考查了复数代数形式的乘除运算,考查了复数的基本概念,是基础题.

练习册系列答案
相关题目
10.已知函数f(x)=|xex|,方程f2(x)-tf(x)+1=0(t∈R)有四个实数根,则t的取值范围为( )
| A. | $(\frac{{{e^2}+1}}{e},+∞)$ | B. | $(-∞,-\frac{{{e^2}+1}}{e})$ | C. | $(-\frac{{{e^2}+1}}{e},-2)$ | D. | $(2,\frac{{{e^2}+1}}{e})$ |
20.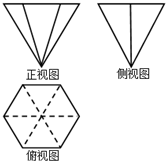 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )
 一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )
一个几何体的三视图如图所示,其中正视图是边长为2的等边三角形,俯视图为正六边形,则该几何体的侧视图的面积是( )| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | $\frac{3}{2}$ |
7.已知集合A={a,b},B={c,d,e},从A到B的不同映射个数是( )
| A. | 6 | B. | 8 | C. | 9 | D. | 5 |