题目内容
 如图,底面为正方形的四棱锥S-ABCD 中,P为侧棱SD上的点且SD⊥平面PAC,每条侧棱的长都是底面边长的
如图,底面为正方形的四棱锥S-ABCD 中,P为侧棱SD上的点且SD⊥平面PAC,每条侧棱的长都是底面边长的| 2 |
(1)求二面角P-AC-D的大小.
(2)在侧棱SC上是否存在一点E,使得BE∥平面PAC.若存在,求SE:EC的值;若不存在,试说明理由.
考点:与二面角有关的立体几何综合题
专题:空间位置关系与距离,空间角
分析:(1)利用二面角的定义作出二面角的平面角,知AC⊥平面SBD,所以AC⊥OP,且AC⊥OD,所以∠POD是二面角P-AC-D的平面角,或用向量法;
(2)利用线面平行的性质解决,或用向量法.
(2)利用线面平行的性质解决,或用向量法.
解答:
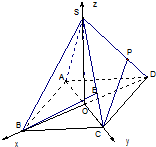
 解法一:
解法一:
(1)连BD,设AC交BD于O,由题意SO⊥AC.在正方形ABCD中,AC⊥BD,所以AC⊥平面SBD,得AC⊥SD.
设正方形边长a,则SD=
a.
又OD=
a,所以∠SOD=60°,
连OP,知AC⊥平面SBD,所以AC⊥OP,
且AC⊥OD,所以∠POD是二面角P-AC-D的平面角.
由SD⊥平面PAC,知SD⊥OP,所以∠POD=30°,
即二面角P-AC-D的大小为300.
(2)在棱SC上存在一点E,使BE∥平面PAC
由(1)可得PD=
a,故可在SP上取一点N,使PN=PD,过N作PC的平行线与SC的交点即为E.连BN.
在△BDN中知BN∥PO,又由于NE∥PC,故平面BEN∥平面PAC,得BE∥平面PAC,由于SN:NP=2:1,故SE:EC=2:1.
解析二(1)连BD,设AC交于BD于O,由题意知SO⊥平面ABCD.
以O为坐标原点,
,
,
分别为x轴、y轴、z轴正方向,建立坐标系O-xyz如图.
…1分
设底面边长为a,则高SO=
a.
于是 S(0,0,
a),D(-
a,0,0),C(0,
a,0)w,B(
a,0,0)
=(0,
a,0)
=(-
a,0,-
a)…3分
由题设知,平面PAC的一个法向量
=(
a,0,
a),平面DAC的一个法向量
=(0,0,
a),
设所求二面角为θ,则cosθ=
=
,θ∈[0,π]
∴θ=
故所求二面角的大小为
…7分
(2)在棱SC上存在一点E使BE∥平面PAC.
由(1)知
是平面PAC的一个法向量,
且
=(
a,0,
a),
=(0,-
a,
a),
=(-
a,
a,0)
设
=t
,则
=
+
=
+t
=(-
a,
a(1-t),
at)
而
•
=0?t=
即当SE:EC=2:1时,
⊥
而BE不在平面PAC内,故BE∥平面PAC…12分.

 解法一:
解法一:(1)连BD,设AC交BD于O,由题意SO⊥AC.在正方形ABCD中,AC⊥BD,所以AC⊥平面SBD,得AC⊥SD.
设正方形边长a,则SD=
| 2 |
又OD=
| ||
| 2 |
连OP,知AC⊥平面SBD,所以AC⊥OP,
且AC⊥OD,所以∠POD是二面角P-AC-D的平面角.
由SD⊥平面PAC,知SD⊥OP,所以∠POD=30°,
即二面角P-AC-D的大小为300.
(2)在棱SC上存在一点E,使BE∥平面PAC
由(1)可得PD=
| ||
| 4 |
在△BDN中知BN∥PO,又由于NE∥PC,故平面BEN∥平面PAC,得BE∥平面PAC,由于SN:NP=2:1,故SE:EC=2:1.
解析二(1)连BD,设AC交于BD于O,由题意知SO⊥平面ABCD.
以O为坐标原点,
. |
| OB |
. |
| OC |
. |
| OS |
…1分
设底面边长为a,则高SO=
| ||
| 2 |
于是 S(0,0,
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
. |
| OC |
| ||
| 2 |
. |
| SD |
| ||
| 2 |
| ||
| 2 |
由题设知,平面PAC的一个法向量
. |
| DS |
| ||
| 2 |
| ||
| 2 |
. |
| OS |
| ||
| 2 |
设所求二面角为θ,则cosθ=
| ||||
|
|
| ||
| 2 |
∴θ=
| π |
| 6 |
| π |
| 6 |
(2)在棱SC上存在一点E使BE∥平面PAC.
由(1)知
. |
| DS |
且
. |
| DS |
| ||
| 2 |
| ||
| 2 |
. |
| CS |
| ||
| 2 |
| ||
| 2 |
. |
| BC |
| ||
| 2 |
| ||
| 2 |
设
. |
| CE |
. |
| CS |
. |
| BE |
. |
| BC |
. |
| CE |
. |
| BC |
. |
| CS |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
而
. |
| BE |
. |
| DS |
| 1 |
| 3 |
即当SE:EC=2:1时,
. |
| BE |
. |
| DS |
而BE不在平面PAC内,故BE∥平面PAC…12分.
点评:本题主要考查了直线与平面平行的判定,以及空间两直线的位置关系的判定和二面角的求法,涉及到的知识点比较多,知识性技巧性都很强.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
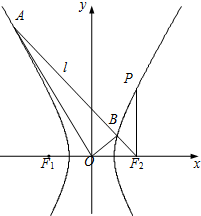 设点P在以F1、F2为左、右焦点的双曲线C:
设点P在以F1、F2为左、右焦点的双曲线C: