题目内容
5.过点M(0,2)的直线l与抛物线y2=-4x交于A,B两点,与x轴交于点C,则有( )| A. | |MA|+|MB|=2|MC| | B. | |MA|•|MB|=|MC|2 | C. | |MA|=|MB|•|MC| | D. | |MA|2=|MB|2+|MC|2 |
分析 可画出图形,设l的方程为y=kx+2,从而可联立抛物线的方程消去x得到${y}^{2}+\frac{4}{k}•y-\frac{8}{k}=0$,可设A(x1,y1),B(x2,y2),根据韦达定理即可求出${x}_{1}{x}_{2}=\frac{4}{{k}^{2}}$,根据图形可以得到$\frac{|MA|}{|MC|}=\frac{-{x}_{1}}{\frac{2}{k}},\frac{|MC|}{|MB|}=\frac{\frac{2}{k}}{-{x}_{2}}$,这样便可得到$\frac{|MA|}{|MC|}=\frac{|MC|}{|MB|}$,从而找出正确选项.
解答 解:如图,设直线l的方程为y=kx+2,∴$x=\frac{y-2}{k}$,代入抛物线方程并整理得: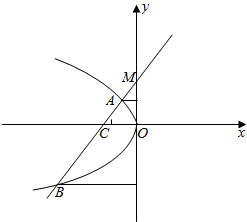
${y}^{2}+\frac{4}{k}•y-\frac{8}{k}=0$;
设A(x1,y1),B(x2,y2),则${y}_{1}+{y}_{2}=-\frac{4}{k},{y}_{1}{y}_{2}=-\frac{8}{k}$;
∴${x}_{1}{x}_{2}=\frac{{y}_{1}-2}{k}•\frac{{y}_{2}-2}{k}$=$\frac{{y}_{1}{y}_{2}-2({y}_{1}+{y}_{2})+4}{{k}^{2}}=\frac{4}{{k}^{2}}$;
∵$C(-\frac{2}{k},0)$;
∴$\frac{|MA|}{|MC|}=\frac{-{x}_{1}}{\frac{2}{k}}=\frac{{x}_{1}{x}_{2}}{\frac{2}{k}•(-{x}_{2})}=\frac{\frac{4}{{k}^{2}}}{\frac{2}{k}•(-{x}_{2})}$,$\frac{|MC|}{|MB|}=\frac{\frac{2}{k}}{-{x}_{2}}=\frac{\frac{4}{{k}^{2}}}{(-{x}_{2})•\frac{2}{k}}$;
∴$\frac{|MA|}{|MC|}=\frac{|MC|}{|MB|}$;
∴|MA||MB|=|MC|2.
故选:B.
点评 考查直线的点斜式方程,椭圆的标准方程,韦达定理,以及相似三角形对应边的比例关系.

| A. | 1 | B. | 3 | C. | 11 | D. | 13 |
| A. | y=-sin2x | B. | y=sin(2x+$\frac{π}{4}$) | C. | y=-cos2x | D. | y=cos2x |
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
| A. | 4$\sqrt{6}$π | B. | 2$\sqrt{6}$π | C. | 16$\sqrt{3}$π | D. | 8$\sqrt{6}$π |