题目内容
已知椭圆
+y2=1右焦点为F2,过F2的直线l交椭圆于A,B两点.若椭圆上一点P可使
+
+
=
,求P点坐标.
| x2 |
| 2 |
| OA |
| OB |
| OP |
| 0 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:过F2的直线l的方程为y=k(x-1),由
,得:(2k2+1)x2-4k2x+2k2-2=0.设A(x1,y1),B(x2,y2),则x1+x2=
,y1+y2=-
,设P(m,n),由
+
+
=
,P(m,n)在椭圆上,推导出
+(
)2=1,由此能求出P点坐标.
|
| 4k2 |
| 2k2+1 |
| 2k |
| 2k2+1 |
| OA |
| OB |
| OP |
| 0 |
(-
| ||
| 2 |
| 2k |
| 2k2+1 |
解答:
解:∵椭圆
+y2=1右焦点为F2(1,0),
∴过F2的直线l的方程为x=1或y=k(x-1),
当x=1时,
+
=
,使
+
+
=
的点P不存在,
∴x=1不成立.
联立
,消去y,并整理,得:(2k2+1)x2-4k2x+2k2-2=0.
设A(x1,y1),B(x2,y2),则x1+x2=
,x1x2=
,
∴y1+y2=k(x1+x2)-2k=
-
=-
,
设P(m,n),∵
+
+
=
,P(m,n)在椭圆上,
∴
,且
+(
)2=1,
解得k=±
,
当k=
时,m=-1,n=
,P(-1,
);
当k=-
时,m=-1,n=-
,P(-1,-
).
∴P点坐标为P(-1,
)或P(-1,-
).
| x2 |
| 2 |
∴过F2的直线l的方程为x=1或y=k(x-1),
当x=1时,
| OA |
| OB |
| OF |
| OA |
| OB |
| OP |
| 0 |
∴x=1不成立.
联立
|
设A(x1,y1),B(x2,y2),则x1+x2=
| 4k2 |
| 2k2+1 |
| 2k2-2 |
| 2k2+1 |
∴y1+y2=k(x1+x2)-2k=
| 4k3 |
| 2k2+1 |
| 4k3+2k |
| 2k2+1 |
| 2k |
| 2k2+1 |
设P(m,n),∵
| OA |
| OB |
| OP |
| 0 |
∴
|
(-
| ||
| 2 |
| 2k |
| 2k2+1 |
解得k=±
| 1 | ||
|
当k=
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
当k=-
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
∴P点坐标为P(-1,
| ||
| 2 |
| ||
| 2 |
点评:本题考查椭圆上的点的坐标的求法,是中档题,解题时要认真审题,注意向量知识和椭圆性质的灵活运用.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
已知不等式组
,则其表示的平面区域的面积是( )
|
| A、1 | B、2 | C、3 | D、4 |
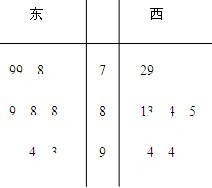 某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.
某城市要建成宜商、宜居的国际化新城,该城市的东城区、西城区分别引进8个厂家,现对两个区域的16个厂家进行评估,综合得分情况如茎叶图所示.