题目内容
9．已知椭圆C1：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$和椭圆C2：$\frac{{x}^{2}}{2}+{y}^{2}$=1的离心率相同，且点（$\sqrt{2}$，1）在椭圆C1上．（1）求椭圆C1的方程；
（2）设P为椭圆C2上一动点，过点P作直线交椭圆C1于A、C两点，且P恰为弦AC的中点．试判断△AOC的面积是否为定值？若是，求出此定值；若不是，说明理由．
分析 （1）运用椭圆的离心率公式和点满足椭圆方程，解方程可得a，b，进而得到椭圆方程；
（2）讨论直线的斜率是否存在，设出直线方程，代入椭圆方程，运用韦达定理和弦长公式，以及点到直线的距离公式，由三角形的面积公式，化简整理，即可得到所求定值．
解答 解：（1）由题意可得，$\frac{2}{{a}^{2}}$+$\frac{1}{{b}^{2}}$=1且$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$，a2-b2=c2，
即a2=4，b2=2，
椭圆C1的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1；
（2）当直线AC的斜率不存在时，
必有P（±$\sqrt{2}$，0），此时|AC|=2，S△AOC=$\sqrt{2}$；
当直线AC的斜率存在时，设其斜率为k、点P（x0，y0），
则AC：y-y0=k（x-x0），
与椭圆C1联立，得（1+2k2）x2+4k（y0-kx0）x+2（y0-kx0）2-4=0，
设A（x1，y1），C（x2，y2），则x0=$\frac{{x}_{1}+{x}_{2}}{2}$=-$\frac{2k（{y}_{0}-k{x}_{0}）}{1+2{k}^{2}}$，
即x0=-2ky0，又x02+2y02=2，y02=$\frac{1}{1+2{k}^{2}}$，
S△AOC=$\frac{1}{2}$•$\frac{|{y}_{0}-k{x}_{0}|}{\sqrt{1+{k}^{2}}}$•$\sqrt{1+{k}^{2}}$•$\frac{\sqrt{16{k}^{2}（{y}_{0}-k{x}_{0}）^{2}-4（1+2{k}^{2}）[2（{y}_{0}-k{x}_{0}）^{2}-4]}}{1+2{k}^{2}}$
=$\sqrt{2}$•$\frac{|{y}_{0}-k{x}_{0}|\sqrt{2（1+2{k}^{2}）-（{y}_{0}-k{x}_{0}）^{2}}}{1+2{k}^{2}}$
=$\sqrt{2}$•$\frac{（1+2{k}^{2}）|{y}_{0}|\sqrt{2（1+2{k}^{2}）-（1+2{k}^{2}）}}{1+2{k}^{2}}$
=$\sqrt{2}$|y0|•$\sqrt{1+2{k}^{2}}$=$\sqrt{2}$．
综上，无论P怎样变化，△AOC的面积为常数$\sqrt{2}$．
点评 本题考查椭圆的方程的求法，注意运用离心率公式和点满足椭圆方程，考查三角形的面积的求法，注意讨论直线的斜率是否存在，联立直线和椭圆方程，运用韦达定理和弦长公式，考查化简整理的运算能力，属于中档题．
| A． | 直线a，b都平行于同一个平面 | B． | 直线a平行于直线b所在的平面 | ||
| C． | 直线a，b都垂直于同一条直线 | D． | 直线a，b都垂直于同一个平面 |
| A． | -8 | B． | 10 | C． | 12 | D． | 15 |
| A． | a≥2 | B． | a＞2 | C． | a≥1 | D． | a＞1 |
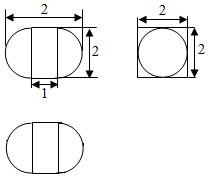
| A． | $4+\frac{2π}{3}$ | B． | $8+\frac{2π}{3}$ | C． | $4+\frac{4π}{3}$ | D． | $6+\frac{4π}{3}$ |