题目内容
20.已知平面向量$\overrightarrow a$与$\overrightarrow b$的夹角为60°,$\overrightarrow a=(2,0)$,$|{\overrightarrow b}$|=1,则$|{\overrightarrow a+2\overrightarrow b}$|=2$\sqrt{3}$.分析 计算$\overrightarrow{a}•\overrightarrow{b}$,再计算($\overrightarrow{a}+2\overrightarrow{b}$)2,开方即可得出$|{\overrightarrow a+2\overrightarrow b}$|.
解答 解:|$\overrightarrow{a}$|=2,$\overrightarrow{a}•\overrightarrow{b}$=|$\overrightarrow{a}$||$\overrightarrow{b}$|cos60°=2×$1×\frac{1}{2}$=1.
∴($\overrightarrow{a}+2\overrightarrow{b}$)2=${\overrightarrow{a}}^{2}+4\overrightarrow{a}•\overrightarrow{b}+4{\overrightarrow{b}}^{2}$=12,
∴$|{\overrightarrow a+2\overrightarrow b}$|=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
相关题目
8.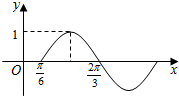 函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )
 函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )
函数f(x)=sin(ωx+φ)(x∈R)$(ω>0,|φ|<\frac{π}{2})$的部分图象如图所示,如果${x_1},{x_2}∈(\frac{π}{6},\frac{2π}{3})$,且f(x1)=f(x2),则f(x1+x2)=( )| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
5.已知直线l:y=kx+b,曲线C:x2+y2=1,则“b=1”是“直线l与曲线C有公共点”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.已知函数$f(x)=\left\{{\begin{array}{l}{x+6,x≤2}\\{{3^x}-1,x>2}\end{array}}\right.$,若f(a)=80,则f(a-4)=( )
| A. | 0 | B. | 3 | C. | 6 | D. | 9 |
10.设x、y满足约束条件$\left\{\begin{array}{l}{x-2y+2≥0}\\{3x-2y-6≤0}\\{x≥0,y≥0}\end{array}\right.$若目标函数z=ax+by(a>0,b>0)的最大值为12,则a2+b2的最小值为( )
| A. | $\frac{25}{4}$ | B. | $\frac{49}{9}$ | C. | $\frac{144}{25}$ | D. | $\frac{225}{49}$ |
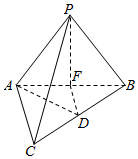 如图,在三棱锥P-ABC中,∠PAC=∠BAC=90°,PA=PB,点D,F分别为BC,AB的中点.
如图,在三棱锥P-ABC中,∠PAC=∠BAC=90°,PA=PB,点D,F分别为BC,AB的中点.