题目内容
解不等式:|x-1|+|x+1|≤4.
考点:绝对值不等式的解法
专题:不等式的解法及应用
分析:由条件利用绝对值的意义求得不等式的解集.
解答:
解:|x-1|+|x+1|表示数轴上的x对应点到1、-1对应点的距离之和,
而2和-2对应点到1、-1对应点的距离之和正好等于4,
故|x-1|+|x+1|≤4的解集为[-2,2].
而2和-2对应点到1、-1对应点的距离之和正好等于4,
故|x-1|+|x+1|≤4的解集为[-2,2].
点评:本题主要考查绝对值的意义,绝对值不等式的解法,属于基础题.

练习册系列答案
相关题目
已知非零向量
,
,则“|
-
|=|
|+|
|”是“
+2
=
”成立的是( )
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| 0 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知a=(log54)2,b=log53,c=ln
,下列结论正确的是( )
| 3 |
| A、a>c>b |
| B、a>b>c |
| C、c>a>b |
| D、b>a>c |
已知函数f(x)=
,若函数F(x)=f(x)-kx有且只有两个零点,则k的取值范围为( )
|
| A、(0,1) | ||
B、(0,
| ||
C、(
| ||
| D、(1,+∞) |
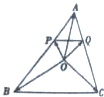 如图,O是△ABC内一点,PQ∥BC,且
如图,O是△ABC内一点,PQ∥BC,且