题目内容
在△ABC中,若BC=a,AC=b,a,b是方程x2-2 x+2=0的两个根,且2cos(A+B)=1,
x+2=0的两个根,且2cos(A+B)=1,
求:(1)角C的度数;
(2)AB的长;
(3)△ABC的面积。
 x+2=0的两个根,且2cos(A+B)=1,
x+2=0的两个根,且2cos(A+B)=1,求:(1)角C的度数;
(2)AB的长;
(3)△ABC的面积。
解:(1)由2cos(A+B)=1,及内角和定理,得cosC=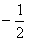 ,
,
所以C=120°;
(2)由a、b是方程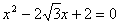 的两个根,
的两个根,
得a+b=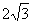 ,ab=2,
,ab=2,
则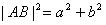 -2abcosC=
-2abcosC=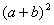 -2ab-2abcos120°=12-4+2=10,
-2ab-2abcos120°=12-4+2=10,
∴|AB|=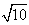 ;
;
(3)S△ABC=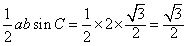 。
。
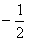 ,
,所以C=120°;
(2)由a、b是方程
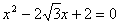 的两个根,
的两个根,得a+b=
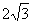 ,ab=2,
,ab=2,则
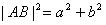 -2abcosC=
-2abcosC=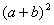 -2ab-2abcos120°=12-4+2=10,
-2ab-2abcos120°=12-4+2=10, ∴|AB|=
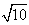 ;
;(3)S△ABC=
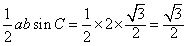 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中,若
=
,
=
,
=
且
•
=
•
=
•
,则△ABC的形状是△ABC的( )
| BC |
| a |
| CA |
| b |
| AB |
| c |
| a |
| b |
| b |
| c |
| c |
| a |
| A、锐角三角形 |
| B、直角三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
 如图,在△ABC中,若
如图,在△ABC中,若