题目内容
已知a=
，函数f（x）=ax，若实数m，n满足f（m）＞f（n），则m，n的大小关系为 ．
| ||||
| 2 |
考点：不等式比较大小
专题：不等式的解法及应用
分析：由题意可得：函数f（x）=ax在R上是单调减函数，又f（m）＞f（n），可得：m＜n．
解答：
解：因为a=a=
∈（0，1），
所以函数f（x）=ax在R上是单调减函数，
因为f（m）＞f（n），
所以根据减函数的定义可得：m＜n．
故答案为：m＜n．
| ||||
| 2 |
所以函数f（x）=ax在R上是单调减函数，
因为f（m）＞f（n），
所以根据减函数的定义可得：m＜n．
故答案为：m＜n．
点评：解决此类问题的关键是熟练掌握指数函数的单调性与定义，以及单调函数的定义，属于基础题．
练习册系列答案
相关题目
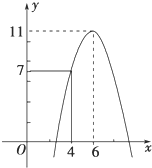某汽车运输公司购买了一批豪华大客车投入运营．据市场分析，每辆客车营运的总利润y（单位：10万元）与营运年数x（x∈N+）为二次函数的关系（如图），要使营运的年平均利润最大，则每辆客车营运年数为
关于方程|log2x|=a（a＞0）的两个根x1，x2（x1＜x2）以下说法正确的是（ ）
| A、x1+x2＞3 |
| B、x1x2＞2 |
| C、x1x2=1 |
| D、1＜x1+x2＜2 |