题目内容
已知两点F1(-2,0),F2(2,0),动点M在y轴上的射影为N,且满足2•
•
=
2
(1)求动点M的轨迹C的方程;
(2)A,B是轨迹C上的两点,AB中点S的横坐标为1,求|AB|的最大值,并求此时直线AB的方程.
| MF1 |
| MF2 |
| MN |
(1)求动点M的轨迹C的方程;
(2)A,B是轨迹C上的两点,AB中点S的横坐标为1,求|AB|的最大值,并求此时直线AB的方程.
考点:轨迹方程,直线的一般式方程
专题:向量与圆锥曲线
分析:(1)设出M的坐标,求出向量
,
,
的坐标,代入2•
•
=
2求得动点M的轨迹C的方程;
(2)求出椭圆的右焦点坐标,离心率e=
和右准线方程,设点A,B及中点S在右准线上的射影分别为A1,B1,S1,则|SS1|=3,然后由向量模间的关系求得|AB|的最大值,再设S(1,y0),A (x1,y1),
B(x2,y2),由点差法求得AB的斜率,再由kAB=kSF2求得S的纵坐标,则直线方程可求.
| MF1 |
| MF2 |
| MN |
| MF1 |
| MF2 |
| MN |
(2)求出椭圆的右焦点坐标,离心率e=
| ||
| 2 |
B(x2,y2),由点差法求得AB的斜率,再由kAB=kSF2求得S的纵坐标,则直线方程可求.
解答:
解:(1)设M(x,y),
又F1(-2,0),F2(2,0),
则
=(-2-x,-y),
=(2-x,-y).
由2•
•
=
2可得2[(x+2)(x-2)+y2]=x2,
化简得x2+2y2=8,即动点M的坐标满足于方程
+
=1;
(2)椭圆
+
=1的右焦点为(2,0),离心率e=
,右准线为:x=4
设点A,B及中点S在右准线上的射影分别为A1,B1,S1,则|SS1|=3,
|AA1|+|BB1|=2|SS1|=6,|AF2|+|BF2|=e(|AA1|+|BB1|)=3
,
|AB|≤|AF2|+|BF2|=3
,当AB过右焦点时取等号,
∴|AB|的最大值是3
,此时,AB过右焦点(2,0),
设S(1,y0),A (x1,y1),B(x2,y2),则
x12+2y12=8,x22+2y22=8,
两式相减,得(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0.
将x1+x2=2,y1+y2=2y0代入上式,可得 (x1-x2)+2y0(y1-y2)=0,
由|AB|=3
知y0≠0,x1≠x2,
∴kAB=
=-
,
又kAB=kSF2=
=-y0,
∴y02=
,y0=±
.
当y0=
时,kAB=-
,
直线方程为x+
y-2=0;
当y0=-
时,kAB=
,
直线方程为x-
y-2=0
又F1(-2,0),F2(2,0),
则
| MF1 |
| MF2 |
由2•
| MF1 |
| MF2 |
| MN |
化简得x2+2y2=8,即动点M的坐标满足于方程
| x2 |
| 8 |
| y2 |
| 4 |
(2)椭圆
| x2 |
| 8 |
| y2 |
| 4 |
| ||
| 2 |
设点A,B及中点S在右准线上的射影分别为A1,B1,S1,则|SS1|=3,
|AA1|+|BB1|=2|SS1|=6,|AF2|+|BF2|=e(|AA1|+|BB1|)=3
| 2 |
|AB|≤|AF2|+|BF2|=3
| 2 |
∴|AB|的最大值是3
| 2 |
设S(1,y0),A (x1,y1),B(x2,y2),则
x12+2y12=8,x22+2y22=8,
两式相减,得(x1+x2)(x1-x2)+2(y1+y2)(y1-y2)=0.
将x1+x2=2,y1+y2=2y0代入上式,可得 (x1-x2)+2y0(y1-y2)=0,
由|AB|=3
| 2 |
∴kAB=
| y1-y2 |
| x1-x2 |
| 1 |
| 2y0 |
又kAB=kSF2=
| y0 |
| 1-2 |
∴y02=
| 1 |
| 2 |
| ||
| 2 |
当y0=
| ||
| 2 |
| ||
| 2 |
直线方程为x+
| 2 |
当y0=-
| ||
| 2 |
| ||
| 2 |
直线方程为x-
| 2 |
点评:本题考查了椭圆分析的求法,考查了直线与圆锥曲线的关系,关键是向量的模的运算,着重体现了设而不求的解题思想方法,是压轴题.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
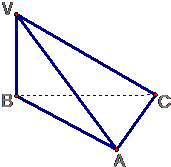
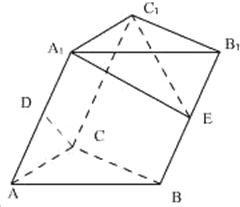 在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥面ABC,AA1=
在斜三棱柱ABC-A1B1C1中,侧面ACC1A1⊥面ABC,AA1=