题目内容
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
)P(
,3),Q(
,-3)分别是f(x)图象上相邻的最高点和最低点.
(1)求f(x)的解析式;
(2)用“五点法”作出f(x)在一个周期内的图象;
(3)若θ∈(0,π),且f(θ)>
,求θ的取值范围.
| π |
| 2 |
| 5π |
| 12 |
| 11π |
| 12 |
(1)求f(x)的解析式;
(2)用“五点法”作出f(x)在一个周期内的图象;
(3)若θ∈(0,π),且f(θ)>
| 3 |
| 2 |
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,五点法作函数y=Asin(ωx+φ)的图象
专题:三角函数的图像与性质
分析:(1)直接根据三角函数图象过点P、Q求解即可;
(2)利用五点法画出图象即可;
(3)首先,求解三角不等式,然后,结合给定的范围求解即可.
(2)利用五点法画出图象即可;
(3)首先,求解三角不等式,然后,结合给定的范围求解即可.
解答:
解:(1)∵函数过点P(
,3),Q(
,-3),
∴A=3,
由题意,得
T=
,∴T=π,
∴
=π,
∴ω=2,
∴f(x)=3sin(2x+φ),
将点P(
,3)代人,得
3sin(
+φ)=3,|φ|<
,
∴φ=-
,
∴f(x)=3sin(2x-
),
(2)根据五点法画图,得
当2x-
=0,即x=
时,y=0;
当2x-
=
,即x=
时,y=3;
当2x-
=π,即x=
时,y=0;
当2x-
=
,即x=
时,y=-3;
当2x-
=2π,即x=
时,y=0,
如下表所示:
对应的图象如下图所示:
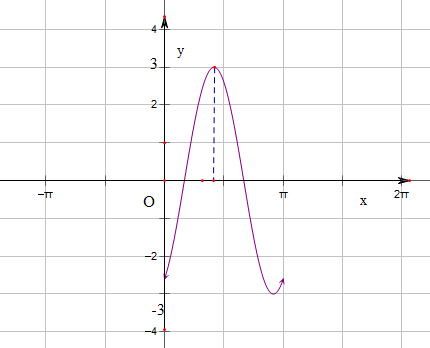
(3)∵f(θ)=3sin(2θ-
)>
,
∴sin(2θ-
)>
,
∴
+kπ≤x≤
+2kπ,k∈Z,
∵θ∈(0,π),
∴所求θ的取值范围(
,
),
| 5π |
| 12 |
| 11π |
| 12 |
∴A=3,
由题意,得
| 1 |
| 2 |
| π |
| 2 |
∴
| 2π |
| ω |
∴ω=2,
∴f(x)=3sin(2x+φ),
将点P(
| 5π |
| 12 |
3sin(
| 5π |
| 6 |
| π |
| 2 |
∴φ=-
| π |
| 3 |
∴f(x)=3sin(2x-
| π |
| 3 |
(2)根据五点法画图,得
当2x-
| π |
| 3 |
| π |
| 6 |
当2x-
| π |
| 3 |
| π |
| 2 |
| 5π |
| 12 |
当2x-
| π |
| 3 |
| 2π |
| 3 |
当2x-
| π |
| 3 |
| 3π |
| 2 |
| 11π |
| 12 |
当2x-
| π |
| 3 |
| 7π |
| 6 |
如下表所示:
2x-
| 0 |
| π |
| 2π | ||||||||||
| x |
|
|
|
|
| ||||||||||
y=3sin(2x-
| 0 | 3 | 0 | -3 | 0 |

(3)∵f(θ)=3sin(2θ-
| π |
| 3 |
| 3 |
| 2 |
∴sin(2θ-
| π |
| 3 |
| 1 |
| 2 |
∴
| π |
| 4 |
| 7π |
| 12 |
∵θ∈(0,π),
∴所求θ的取值范围(
| π |
| 4 |
| 7π |
| 12 |
点评:本题重点考查了三角函数的图象与性质、三角函数的五点法作图、三角不等式等知识,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
△ABC中,点D在AB上,CD平分∠ACB.若
=
,
=
,|
|=2,|
|=1,
=( )
| CA |
| a |
| CB |
| b |
| a |
| b |
| CD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
已知平面内M,N,P三点满足
-
+
=0,则下列说法正确的是( )
| MN |
| PN |
| PM |
| A、M,N,P是一个三角形的三个顶点 |
| B、M,N,P是一个直线上的三个点 |
| C、M,N,P是平面内任意的三个点 |
| D、以上都不对 |