题目内容
17．如图，若下列程序执行的结果是2，则输入的x值是（ ）
| A． | 2 | B． | -2 | C． | 2或-2 | D． | 0 |
分析 由已知中的程序框图可得，该程序的功能是利用条件结构计算并输出分段函数y=$\left\{\begin{array}{l}x，x≥0\\-x，x＜0\end{array}\right.$=|x|的值，进而得到答案．
解答 解：由已知中的程序框图可得，该程序的功能是利用条件结构计算并输出分段函数y=$\left\{\begin{array}{l}x，x≥0\\-x，x＜0\end{array}\right.$=|x|的值，
若输出结果为2，
则|x|=2，
则x=2或x=-2，
故选：C
点评 本题考查的知识点是程序框图，分段函数的应用，难度不大，属于基础题．
练习册系列答案
相关题目
7．若执行如图所示的程序，输出的结果为48，则判断框中应填入的条件为（ ）
| A． | i≥6？ | B． | i＞6？ | C． | i≥4？ | D． | i＞4？ |
8．与向量$\overrightarrow{a}$=（1，3，-2）平行的一个向量的坐标是（ ）
| A． | （$\frac{1}{3}$，1，1） | B． | （-$\frac{1}{2}$，-$\frac{3}{2}$，1） | C． | （-$\frac{1}{2}$，$\frac{3}{2}$，-1） | D． | （$\sqrt{2}$，-3，-2$\sqrt{2}$） |
5．函数y=lnx-6+2x的零点为x0，x0∈（ ）
| A． | （1，2） | B． | （2，3） | C． | （3，4） | D． | （5，6） |
12．
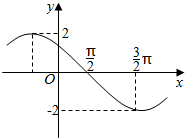已知f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，则f（x）解析式是（ ）
已知f（x）=Asin（ωx+φ），（A＞0，ω＞0，0＜φ＜π）的图象的一部分如图所示，则f（x）解析式是（ ）| A． | f（x）=2sin（$\frac{1}{2}$x-$\frac{π}{4}$） | B． | f（x）=2sin（$\frac{1}{2}$x+$\frac{3π}{4}$） | C． | f（x）=2sin（2x-$\frac{π}{4}$） | D． | f（x）=2sin（2x+$\frac{3π}{4}$） |